Calcular a área do triângulo de vértices
Passo 1
Temos os vértices de um triângulo que são os pontos . Com esses pontos devemos determinar a área do triângulo.
Na teoria vimos como calcular a área de um paralelogramo, então sucesso, já sabemos como fazer. Opa! Mas, aqui é a aréa de um triângulo!!! Como faremos?

Ahh precisamos de uma informação valiosa lá do colégio. Quando aprendemos que a área de um paralelogramo é duas vezes a área de um triângulo. Então, temos que:
Passo 2
Então, a área do paralelogramo sabemos calcular!
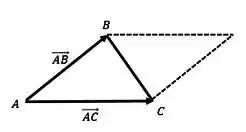
Pela figura, temos os vértices do triângulo . Para calcular a área do paralelogramo formado pelos vetores , sabemos pela teoria que equivale ao módulo do produto vetorial entre esses dois vetores:
Então, primeiro precisamos calcular o produto vetorial. Mas, antes precisamos calcular os vetores , pois foi nos dado os pontos apenas.
Agora sim, podemos calcular o produto vetorial:
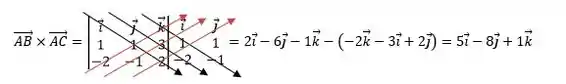
Passo 3
Agora que temos o produto vetorial, vamos calcular o módulo do vetor, para encontrar a área do paralelogramo.
Passo 4
Mas, não é ainda o que queremos. Queremos a área do triângulo que como falamos antes é:
Então, temos que . Assim:
Depois de fazermos as contas, vamos fazer um questionamento: E se, tivéssemos utilizado, outros vetores, como, por exemplo, alteraria nosso resultado?
O resultado deve ser o mesmo, pois o resultado final é dado em módulo, e esse é igual para qualquer vetor considerado.