Calcule sendo (referidos a uma base ortonormal positiva ).
Passo 1
Vamos aquecer os motores!!!
Bom, o problema pede para calcularmos o produto vetorial , sendo que nos é dado os vetores . Até aí eu entendi!! Mas, e o que quer dizer a frase “referidos a uma base ortonormal positiva ”?
Bem, ela só nos diz que devemos considerar a base cartesiana, é mais para reforçar mesmo, porque dificilmente trabalhamos com outras bases, só mais para frente veremos. Mas, isso vemos depois, foco aqui!
Passo 2
Agora é aplicar o que vimos na teoria, montar o determinante direitinho e depois resolvê-lo.
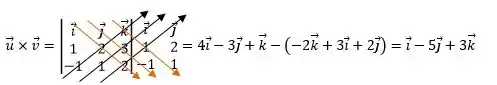
Então,
Lembrando, o produto gera um vetor.
Resposta
Exercícios de Livros Relacionados
Se u é um vetor unitário, determine u . v e u . w
Um vendedor vende a hambúrgueres, b cachorros-quentes e c refrigerantes em um determinado dia. Ele cobra $2 o hambúrgues, $1,50 o cachorro-quente e $1 o refrigerante. Se A =a , b , c e P =2 ,1,5 ,1 ,
Para que valores de b os vetores - 6 , b , 2 e b , b^2 , b são ortogonais?
Calcule | u ×v | e determine se u ×v tem sentido de entrar ou sair da página.
Encontre o vetor, não com determinantes, mas usando propriedades do produto vetorial. k × ( i - 2 j )