Determinar um vetor unitário simultaneamente ortogonal aos vetores e . Nas mesmas condições, determine um vetor de módulo 5.
Passo 1
O problema nos dá dois vetores e . Com esses dois vetores devemos determinar um vetor que seja ortogonal aos dois vetores dados e além disso, que seja unitário.
Bom, no exercício anterior vimos que se realizarmos o produto vetorial entre e , o vetor resultante será ortogonal a esses dois vetores. Okay, essa parte já entendemos!! E o unitário onde entra nessa história?

Calma!! Você vai entender tudinho!!
Na teoria não chegamos a falar sobre o termo “unitário”, mas ele significa que o módulo do vetor deve ser unitário. Assim, esse vetor é chamado de “versor”. Para achar o vetor unitário basta calcular o seu módulo e dividir cada coordenada pelo seu módulo, assim oh:
Passo 2
Agora, é fazermos as conta. Vamos começar resolvendo o produto vetorial :
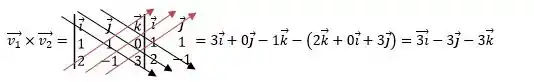
Achamos o vetor que queríamos, que é . Agora falta transformá-lo em unitário.
Passo 3
Então, para fazê-lo ter módulo unitário, vamos calcular primeiro o seu módulo, que é:
O vetor unitário que estamos procurando será:
É bom lembrar que se considerarmos , obteremos como resultado o oposto do vetor obtido anteriormente, pois:
Passo 4
Já temos o vetor unitário, agora queremos calcular um vetor de módulo cinco nas mesmas condições do anterior. Se nas mesmas condições do anterior podemos utilizar o resultado que temos.
Vamos pensar um pouco... Se o vetor que encontramos é unitário, ou seja, seu módulo é unitário, então, isso significa que se multiplicarmos as suas coordenadas por , o vetor passará a ter módulo ?

É exatamente isso. Então, o vetor de módulo é: