A2 T7 T9
Andrezinho respondeu à questão “Prove que, para todo subespaço vetorial , tem-se que da seguinte maneira:
Sejam e dois subespaços vetoriais de . Defina .
Defina “a soma dos subespaços vetoriais e é direta”.
Andrezinho escreveu apenas uma demonstração parcial. O que falta na demonstração dele?
Passo 1
Letra
Basta trocar por e por .
Passo 2
Letra
Repare que o enunciado pede a definição da soma ser direta, e não quando um espaço vetorial é soma de outros dois subespaços.
Basta trocar por .
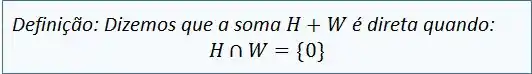
Passo 3
-
Letra
Como no enunciado foi pedido para provar que é soma direta de e , pode parecer um pouco implícito mas essa era a ideia, faltou ele provar que . Veja a definição abaixo!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam U e V espaços vetoriais sobre R de dimensões m e n , respectivamente. Considere o espaço vetorial U × V cuja adição é dada por u 1 , v 1 + u 2 , v 2 = u 1 + u 2 , v 1 + v 2 E a multiplicação por
Sendo W o sub-espaço do exercício 1 e U o sub-espaço do R 4 gerado por 1 ,2 ,1 ,3 e ( 3 ,1 ,- 1 ,4 ) , determinar uma base e a dimensão de U + W e de U ∩ W .
Suponha que { u 1 , … ,u n } é uma base de um espaço vetorial. Mostrar que { u 1 ,u 1 + u 2 , … ,u 1 + u 2 + … + u n } também é uma base desse espaço.
Determinar a dimensão dos seguintes subespaços de M n ( R ) :Subespaço da matrizes simétricas;Subespaço das matrizes antissimétricas.Subespaço das matrizes A tais que A = 2 A t .Subespaço das matrizes
No espaço vetorial R 3 consideremos os seguintes sub-espaços: U = x ,y ,z x = 0 , V = x ,y ,z y - 2 z = 0e W = 1 ,1 ,0 ,0 ,0 ,2 . Determinar uma base e a dimensão de cada um dos seguintes sub-espaços: