Calcule para que o plano seja tangente a , e determine o ponto de tangência.

Sabemos que para que um plano e uma esfera sejam tangentes, precisamos respeitar a relação:

Para acharmos e que respeita a relação acima, temos, primeiro, que encontrar as coordenadas de e o raio . Para isso, vamos analisar a equação da esfera:

Temos, que:

Para calcular a distância vamos usar a fórmula:

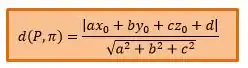
Sendo que da expressão , temos:

Substiutindo temos:

Então,

Vamos fazer o passo a passo para:

Para achar os outros valores é o mesmo esquema ;)

Falta encontrarmos o ponto que é o ponto de tangência. Para achar temos que lembrar da seguinte figura:

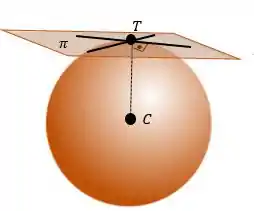
Temos que pertence ao plano , sabemos também que como o plano e a esfera são tangentes, se acharmos duas retas que possuem o ponto essas duas retas serão perpendiculares à reta formada pelo vetor . Se são perpendiculares, podemos usar que:

Então, vamos encontrar dois pontos distintos de e com eles construiremos dois vetores que passam por e que são perpendiculares ao vetor Um ponto para pertencer à deve satisfazer:

Se escolhermos , o valor de . Temos, então nosso primeiro ponto . O segundo ponto pode ser , então . Temos, . Com esses dois pontos podemos construir os vetores:

O vetor é:

Vamos fazer os produtos internos:

Além disso temos que:

Obtemos um sistema:

Substituindo em , temos:

Subsituindo em :

Sendo

Por fim, sabendo que , substuindo em :

Para saber qual é o “correto”, como pertence à deve satisfazer:

Se , então:

Encontramos o ponto .

Ufa!! Terminamos!!