Dadas as esferas
a) Determine o centro e o raio da circunferência .
b) Determine a equação geral do plano que contém .
Passo 1
a) Abrindo os quadrados em :
A intersecção das esferas vai ser dada pelo sistema:
Subtraindo as duas equações:
Esse plano contém a intersecção das esferas.
Passo 2
A circunferência vai ser dada por
O centro de vai ser a projeção do centro de uma das esferas no plano , então:
Dada uma reta perpendicular a e que passe pelo centro de uma das esferas, sua equação será . O centro de vai ser a intersecção da reta com o plano .
Um ponto genérico de é , vamos substituir esse ponto na equação do plano :
Substituindo no ponto genérico, vamos ter que o centro de é
Passo 3
A distância do centro de até o plano é
Na figura abaixo temos a circunferência e o plano . Na intersecção deles temos a circunferência .
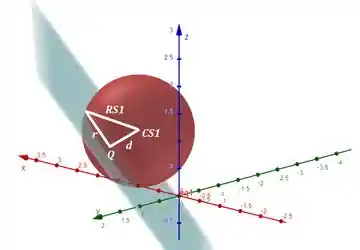
Vamos observar o que raio da circunferência é um cateto de um triângulo retângulo com hipotenusa (raio de ) e o outro cateto é o que acabamos de encontrar. Então
Então o raio de é
Passo 4
b) Opa, já encontramos esse plano na letra a, lá no passo 1 :)
Resposta
a) e
b)