UFPE – Geometria Analítica – 2018.2 – P3 – Questão 2
Seja a superfície esférica que tem por diâmetro o segmento de extremos e .
- Determine uma equação para .
- Determine o centro e o raio da interseção de com o plano .
Passo 1
- Ele deu pra gente os dois extremos do diâmetro. Mas o que é está bem no centro do diâmetro? Pois é, o centro da esfera!
Achamos o centro! Pra achar o raio é só calcular a distancia do centro até um dos extremos do diâmetro! Vamos fazer até o ponto .
Então a equação da esfera vai ser:
Passo 2
b) A interseção da esfera com o plano só pode ser uma circunferência! Pra achar o centro dela, vamos encontrar a interseção de uma reta normal ao plano que passa pelo centro da esfera. Como ela é bem retinha, vai passar também no centro da circunferência! A nossa reta vai ter vetor diretor igual ao vetor normal ao plano, e passa pelo centro da esfera:
Agora vamos achar a interseção dessa reta com o plano .
Assim, o nosso ponto vai ser:
Passo 3
Falta só a gente relacionar o raio da circunferência com o da esfera! Dá uma olhada aqui nessa figura: a gente consegue achar o raio da circunferência por Pitágoras, basta a gente conhecer a distância do centro até o plano!
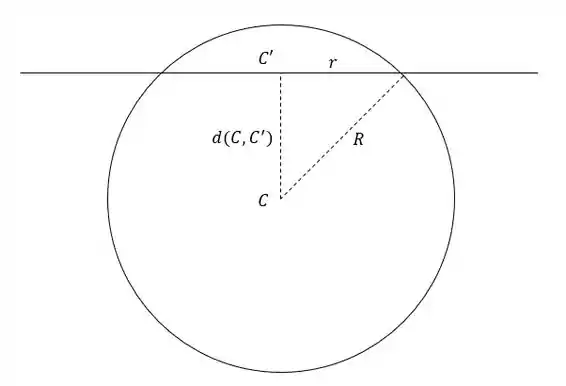
A gente quer a distância do ponto até o plano . Isso aí tem até fórmula!
Agora é só substituir!
Resposta
- ,