Considere a superfície esférica e o plano .
a) Determine o centro e o raio da esfera .
b) Determine os planos paralelos a tais que suas intersecções com resultam em circunferências de raio .
Passo 1
a) Precisamos escrever a equação de em um formato que a gente consiga identificar seu centro e raio. Completando quadrados em e :
Ajustando por produtos notáveis:
Boaa, então concluímos que o centro da esfera é e seu raio é .
Passo 2
b) Vamos pensar de uma forma genérica, imagine o seguinte plano que intersecta a esfera em uma circunferência de raio :
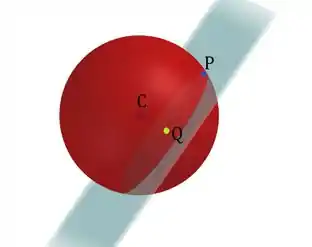
Seja o centro da esfera, o centro da circunferência e um ponto da circunferência, temos um triângulo retângulo em , com hipotenusa e . Fazendo Pitágoras encontramos :
Passo 3
Beleza, então pra esse plano intersectar a esfera em uma circunferência de raio , a distância de até - ou seja, a distância de até o plano que queremos - deve ser 1.
A equação genérica para os planos que estamos procurando é , pois eles são paralelos a e devemos encontrar apenas os possíveis valores de .
Passo 4
Aplicando a fórmula de distância entre ponto e plano e igualando a 1, temos que:
ou
Então, os planos que satisfazem as condições do enunciado são:
Resposta
a) e
b)