Considere a superfície esférica e o plano .
a) Determine o centro e o raio da circunferência
b) Determine as equações paramétricas da reta que passa pelos centros de e .
Passo 1
a) Temos a intersecção da esfera com o plano . Isso vai nos dar uma circunferência certo?
Bom, antes de tudo, vamos encontrar o centro e o raio de . Podemos escrever sua equação assim:
Então o centro de é e o seu raio é
Ah, outra informação que vai ser útil é calcularmos a distância do ponto até o plano :
Bora pros próximos passos então!!
Passo 2
Seja uma reta perpendicular ao plano (ou seja, seu vetor diretor vai ser o vetor normal de ) e que passe pelo ponto .
A equação da reta , de acordo com essas informações, é
Beleza, mas aí, por análise geométrica, a gente repara que o centro da circunferência vai ser a intersecção da reta com o plano , olha:
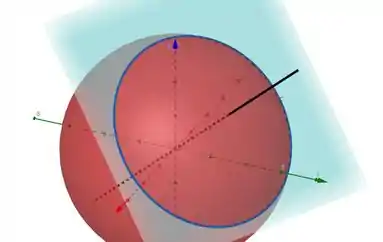
Basicamente: é a projeção de no plano , e a projeção sempre se dá ortogonalmente.
Como a reta é ortogonal ao plano e passa por , sua intersecção com o plano vai dar a projeção ortogonal de , ou seja, o ponto . Deu pra entender? Hehe
Passo 3
Então bora calcular a intersecção da reta com o plano , para encontrarmos o centro da circunferência.
Um ponto genérico de é . Vamos substituir esse ponto na equação do plano:
Substituindo isso no ponto genérico, temos que:
Aeee, já achamos o centro da circunferência, agora só falta o raio :P
Passo 4
Repara uma coisa: os pontos , e um ponto da circunferência formam um triângulo retângulo em com hipotenusa e catetos (aquele lá do passo 1) e (raio da circunferência que queremos descobrir).
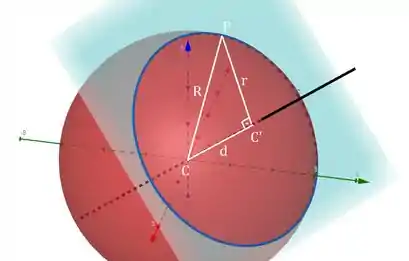
Então é só a gente usar Pitágoras pra encontrarmos nosso certo?
Boa, encontramos nosso centro e nosso raio da circunferência :)
Passo 5
b) Opa, já achamos essa reta no item anterior, é a reta .
A equação paramétrica dela é
E é isso :D
Resposta
a) e
b)