UFPE – Geometria Analítica – 2018.1 – P3 – Questão 5
Considere a curva , onde e .
- Determine o centro e o raio da superfície esférica .
- Mostre que é uma circunferência. Determine também seu centro e raio.
Passo 1
- Bom, galerinha, se você olhar pra , a gente vê que ela tem a cara de uma esfera, certo? A intuição geralmente dá certo! Pra confirmar, vamos desenvolver a expressão completando os quadrados.
- Pra começar, pensa o seguinte: vamos supor que a interseção é uma circunferência de centro . Esse ponto a gente pode achar traçando uma perpendicular ao plano, passando pelo centro da esfera, porque essa reta vai bater bem no meiozinho da seção, e por isso, se for uma circunferência, vai ser o centro dela. Beleza! Essa reta tem vetor diretor , que, como é normal ao plano , é dado por . A gente pode escrever a reta assim:
Então chegamos em:
Isso aí é uma esfera mesmo, com o centro e raio .
Passo 2
E tá justamente nessa reta!
Mas se liga: tá no plano também né? A gente pode botar as coordenadas dele na equação do plano!
Então, substituindo na equação de :
Passo 2
Pra determinar o raio, se liga na figura!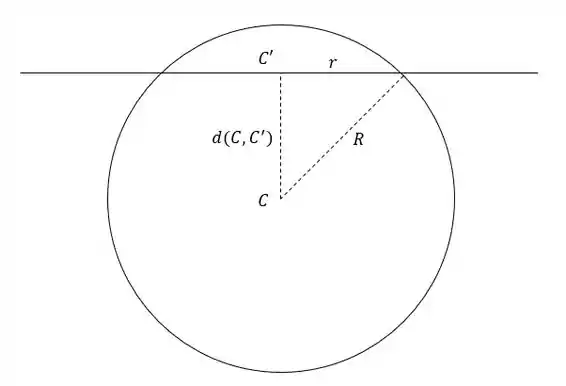
A gente consegue achar ele em função do raio da esfera e da distância entre os centros por Pitágoras, sacou?
Aí, substituindo:
Resposta
- e raio .
- e raio .
Exercícios de Livros Relacionados
Obtenha a equação geral da superfície esférica que contém o ponto A = - 1,6 , - 3 e tangencia o plano π : 4 x + 4 y + 7 z - 96 = 0 em T = 7,3 , 8 .
Determinar uma equação da superfície esférica de centro C ( 2 ,- 3 ,4 ) e:tangente ao plano y O z .
Determinar uma equação das superfícies esféricas nas condições dadas.Centro C ( 2 , - 3,1 ) e raio 4 .
Determinar uma equação das superfícies esféricas nas condições dadas.O segmento de extremos A ( - 1 , 3 , - 5 ) e B ( 5 , - 1 , - 3 ) é um de seus diâmetros.
Determinar uma equação das superfícies esféricas nas condições dadas.O centro C ( - 2 , 3,4 ) e tangente ao eixo O z .