Uma ambulância está trafegando a em uma estrada. Em seguida, ela entra em uma curva, como indicado na figura, com sua velocidade na horizontal. Ao sair da curva, sua velocidade sofre uma mudança de direção, passando a fazer um ângulo de , como mostrado na figura. Determine o módulo, a direção e o sentido da aceleração vetorial média nesse trecho, sabendo que ela demora para fazer essa curva.
Dados: ,
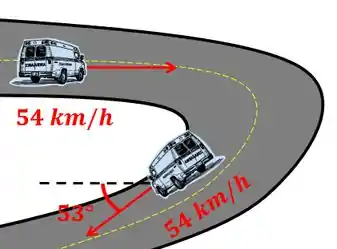
Passo 1
Para acharmos a aceleração vetorial média, podemos usar a fórmula.
Para usar a fórmula devemos, achar a variação do tempo e a variação da velocidade vetorial.
Passo 2
O valor de já temos pelo enunciado, só devemos colocar na unidade correta do SI.
Passo 3
Antes de qualquer coisa, devemos passar o módulo da velocidade de para .
Para isso vamos dividir o valor em por .
Passo 4
Devemos achar agora a variação da velocidade, para isso devemos achar a velocidade vetorial inicial e final. Nesse caso, como os vetores são simples, e o enunciado pede direção e sentido vamos fazer na forma vetorial direto. Começando pela velocidade inicial vetorial.
Passo 5
Agora vamos achar a velocidade final, para isso devemos achar suas componentes decompondo pelo seu módulo e ângulo como fizemos no capítulo de vetores.
Lembrando que para cima/para direita significa sinal positivo, enquanto para baixo/para esquerda significa sinal negativo.
Passo 6
Agora vamos achar ,
Passo 7
A aceleração vetorial média será,
Passo 8
Agora devemos achar o módulo da aceleração.