Em um brinquedo de parque de diversões conhecido como carrinhos de bate-bate, pessoas conduzem pequenos carros envoltos em borracha (de forma que uma colisão entre dois carros é praticamente elástica). Suponha que um carro que contem um adulto de e se desloca a uma velocidade de atinge um carro conduzido por uma criança de se deslocando com a mesma velocidade no sentido contrário. Suponha também que cada carro tem uma inércia de .
- Calcule a velocidade do centro de massa do sistema antes e depois da colisão.
- Considerando que a colisão demora , calcule a aceleração média de cada carrinho durante a colisão e a força média exercida por um carrinho sobre o outro carrinho.
Passo 1
POW! Infelizmente não temos um esqueminha do que está acontecendo aqui, então que tal começarmos por aqui?

No caso, ambos carros tem o mesmo peso, mas como o adulto é mais “pesado” representei o carro maior já que não sei desenhar um adulto kkkk.
Passo 2
Cara! Não sei se você consegue imaginar esse troço, mas tenta viajar um pouco comigo aqui: como o carro que é mais pesado () vai andando em direção ao carro da criança (), o centro de massa vai se deslocando lentamente da esquerda pra direita, já que o carro o mais pesado, e vai da esquerda pra direita (ele tem mais voz ). Saca?
Essa velocidade com que o centro de massa se desloca, vou chamar de , pode ser dada de acordo com a teoria, pela ponderação das velocidades pelas respectivas massas. Ou seja...
Então, como e ...
Repare que no lugar de eu coloquei . O menos, é apenas porque o carro com a criança vai pra trás, então temos que fazer essa consideração, ta ligado?
Bem, com uma calculadora, chegamos então em...
Beleza! Então essa é a velocidade do centro de massa antes da colisão. Mas e depois?
CONTINUA A MESMA! . Afinal, em qualquer sistema isolado não há interferências no centro de massas . Então, para depois da colisão também podemos falar que...
Passo 3
POW! A aceleração média é dada como velocidade final, menos a inicial dividida pelo tempo da colisão . Então, as acelerações médias para cada carro vão ser...
Temos o tempo de colisão e temos também as velocidades iniciais de cada carrinho...
Só fica faltando determinar as velocidades finais mesmo. Bora encontra-las?
Passo 4
Cara! Tipo, sabemos que a colisão é elástica e tals, então a gente até poderia utilizar os conceitos de conservação de momento e colisões elásticas, mas isso seria MUITO trabalhoso. Aqui viu te passar um Bizu, ta bom?
Então, toda vez que a colisão for elástica então podemos prosseguir assim:
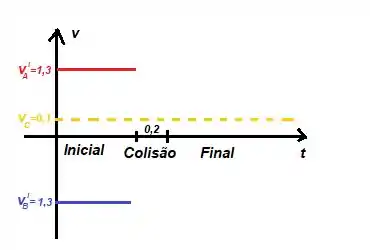
- Primeiro... Você vai construir um gráfico por ...
- Segundo... Você coloca as velocidades iniciais e finais no gráfico até o momento da colisão. Também coloque a velocidade do centro de massa durante todo momento...
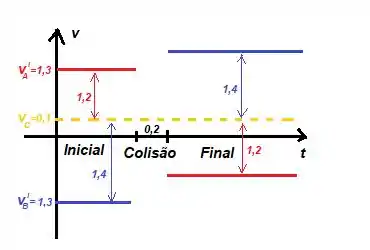
- Terceiro... Pow! Saiba que depois da colisão, as velocidades vão se espelhar com relação à velocidade do centro de massa. Então...
- Finalizando o gráfico...

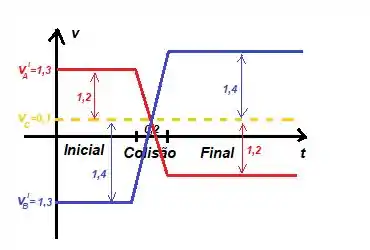
Por esse gráfico, podemos assumir que as velocidades finais de cada carrinho será...
Passo 5
Belezinha, então podemos voltar para onde paramos no passo 4...
E determinar as acelerações médias...
Passo 6
As forças médias exercidas por um carrinho no outro, pode ser dado por Newton ().
Então, a força que o carro do adulto faz sobre o da criança...
E a força que o carro da criança faz sobre o do cara vai ser...
É um par de ação e reação, então já podíamos imaginar que seria a mesma coisa mas com o sinal trocado (sentido oposto).
Resposta
Letra A:
Letra B: