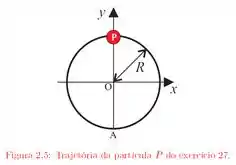
Uma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:
(c) O vetor velocidade média no intervalo do item ;
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o vetor velocidade no intervalo do item (b), que é de a . A velocidade média é dada pelo quociente entre a variação da posição, , e a variação do tempo , ou seja:
Então, vamos usar o vetor deslocamento calculado o item (b) e a variação de tempo dada pela questão para calcular o vetor velocidade.
Vamos lá!
Passo 2
Como no item (b) nós encontramos o vetor deslocamento e temos a variação de tempo:
Então, nossa velocidade média vai ser dada por:
Dividindo as componentes:
Colocando em evidência:
Valeu, galera! Até a próxima! 😉