O trem sai de uma estação a partir do repouso, rumo ao oeste, com aceleração constante de . Já o trem se move do norte para o sul com velocidade constante de , e passa por essa mesma estação segundos após a partida do trem . Considere o versos apontando para leste e o versor para o norte. Considere também a estação na origem do sistema de coordenadas, e considere o tempo inicial no instante em que o trem sai da estação.
Escreva os vetores aceleração, velocidade e posição para os dois trens, em função do tempo e em termos de e .
Qual é o vetor velocidade do trem em relação ao trem em função do tempo?
Passo 1
Eaew, tudo bem com você?
O enunciado nos descreve o movimento de dois trens, o trem que tem uma aceleração de , e a partir do repouso, se move para o oeste saindo de uma estação. O enunciado também indica a existência do trem que vem do norte para o sul à uma velocidade constante de , chegando a estação depois que o trem saiu! O esquema usando os versores indicados no enunciado é o seguinte
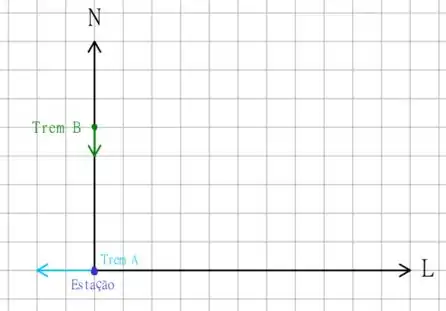
Usando estas informações, é preciso escrever os vetores aceleração, velocidade e posição para cada um dos trens, e obter o vetor velocidade relativa! E como obtemos estes vetores? Vai ser um ponto chave lembrarmos que a aceleração é a taxa de variação instantânea da velocidade, portanto
e, da mesma forma, a velocidade é a taxa de variação da posição
usando ambas estas relações, nós teremos os nossos vetores! A velocidade relativa entre ambos os trens pode ser obtida fazendo
Belezinha? Vamos partir para as continhas! Bora lá!
Passo 2
Vamos começar escrevendo os vetores aceleração! O trem tem uma aceleração constante na direção oeste, como temos que o referencial é escolhido de forma que aponta para leste, então temos que
para o trem no entanto, temos que sua velocidade é constante, portanto, a aceleração é nula
Maravilha! Agora, vamos encontrar as velocidades!
Passo 3
Vamos trabalhar com a seguinte expressão
se multiplicarmos ambos os lados por , temos que
Se considerarmos que em , temos uma velocidade , e que, para um tempo qualquer , temos uma velocidade , podemos integrar ambos os lados da expressão acima, e obter
usando que
podemos obter que a nossa velocidade é dada por
Agora, precisamos aplicar a expressão acima para ambos trens! Vem comigo!
Passo 4
Para o trem , temos uma aceleração constante , podemos escrever então que
usando que o trem parte do repouso, temos que
da mesma forma, para o trem , temos que
em que temos a velocidade dada no enunciado como
já que o sentido escolhido pelo referencial é positivo na direção norte, e o trem está indo para o sul! Vamos encontrar agora nossas posições!
Passo 5
Da mesma maneira que fizemos para a velocidade, podemos escrever que
se multiplicarmos ambos os lados por , temos que
Se considerarmos que em , temos uma posição , e que, para um tempo qualquer , temos uma posição , podemos integrar ambos os lados da expressão acima, e obter
usando que
podemos obter que a posição é dada por
Vamos aplicar esta expressão para ambos os trens! Saca só!
Passo 6
Temos que o trem começa na estação, que é tomada como origem do sistema de coordenadas, portanto , além disso, podemos usar a velocidade obtida no passo anterior para obter que
lembrando de cálculo , temos que
portanto, nosso vetor posição para o trem , é dada por
Agora temos que fazer o mesmo para o outro trem! Vamos lá!
Passo 7
Vamos chamar a posição do trem de
Note que em , este trem está em uma posição , já que ele não está na origem. Vamos usar as informações dadas no enunciado para encontrar este valor mais tarde! Primeiro, podemos usar a velocidade dada no enunciado para obter que
usando que
ou seja, temos que a velocidade será dada por
Mas como podemos achar ? Note que ele nos diz que após , o trem chega na origem, ou seja, para , temos que , de forma que podemos escrever
Isolando o vetor posição inicial, temos que
Portanto, o vetor posição do trem é simplesmente
Maravilha! Temos as respostas da primeira alternativa! Vamos agora calcular a velocidade relativa para a segunda alternativa!
Passo 8
Usando a definição de velocidade relativa como
usando ambas as velocidades que obtemos nos passos anteriores, temos que
resumindo, temos que
Maravilha! As duas primeiras alternativas foram essas! Te vejo jajá nas outras duas! Até logo!
Resposta
Os vetores aceleração são e , os vetores velocidade são e , com velocidade relativa , os vetores posição são e .