USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 29
Uma partícula se desloca, no sentido anti-horário, sobre um círculo de raio , como mostra a figura . Sua velocidade escalar é descrita pela equação . Determine o módulo do vetor aceleração e o ângulo que esse vetor faz com o eixo quando , sabendo que nesse instante a partícula encontra-se na posição indicada na figura .
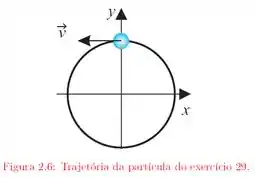
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o módulo da aceleração e o ângulo que ela faz com o eixo quando . Ele nos deu uma trajetória circular de raio e um movimento que é descrito pela equação da velocidade escalar, .
Lembrando que a aceleração também é definida como a derivada da velocidade, nós podemos encontrar o vetor apenas derivando . Calculando o módulo desse vetor, vamos obter a aceleração escalar. Por fim, vamos calcular o ângulo que ela faz com a vertical através da fórmula:
Vamos lá!
Passo 2
Vamos começar derivando para obter:
Como o resultado é constante e não depende do tempo, as componentes do vetor também são constantes. Essas componentes são e . Assim, calculando o módulo do vetor, vamos ter:
E no caso do ângulo, temos:
Valeu, galera! Até a próxima! 😉