Um trem com uma velocidade constante de se move na direção leste por , depois em uma direção que faz um ângulo de a leste com a direção norte por e, finalmente, na direção oeste por mais . Quais são
o módulo e
o ângulo da velocidade média do trem durante a viagem?
Passo 1
Desenhando o trajeto percorrido pelo trem nós teremos algo como:
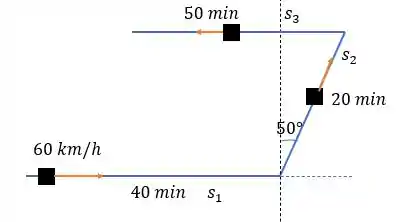
Na letra queremos calcular o módulo da velocidade média desse trem, então tudo o que precisamos calcular é o deslocamento do seu ponto inicial até o final e o temo que esse percurso . A velocidade média é dada por:
Para calcular esse vamos tomar que ele sai da origem e calcular os vetores de posição em cada trecho que o problema nos conta. Partiu!!!
Passo 2
Vamos calcular a posição do objeto no primeiro movimento que ele faz (que é ir para leste durante 40min). Como a velocidade é constante, temos que
Onde é o vetor da distância. Lembrado que representa , logo:
Ou seja, esse cara aí é a posição que ele chega depois dos 40min!
Passo 3
Passo 4
Vamos ver agora aonde ele chega quando começa esse movimento de “subida”. O módulo da velocidade é o mesmo nesse trecho, mas como é um movimento bidimensional, precisamos fazer uma decomposição:
A componente faz com que o trem ande um pouquinho para a direita:
Como a gente viu no primeiro movimento que ele já tinha andado 40km, temos que
A componente faz com que o trem ande um pouquinho para cima:
Então temos:
Passo 5
No terceiro trajeto, o trem só anda na horizontal, então sabemos que ele mantém a componente da posição anterior. A posição horizontal é dada por
Então, o vetor posição do trem no fim do trajeto é:
Passo 6
Como temos a posição final e a posição inicial (que adotamos ser a origem). O Deslocamento total é dado por
O módulo da distância será então igual a:
Passo 7
Na letra queremos o módulo da velocidade do trem e para isso nós temos que fazer:
Onde o tempo percorrido pelo trem em horas será de:
Logo o módulo da velocidade será de:
Passo 8
Como o vetor da velocidade é proporcional ao vetor posição equivalente então podemos afirmar que:
Então o vetor velocidade terá um ângulo de:
E como o tempo é constante e é de ele não faz diferença para a angulação do vetor velocidade resultante, já que a velocidade é constante pra todos os trechos. Também poderia usar a referência angular como sendo: