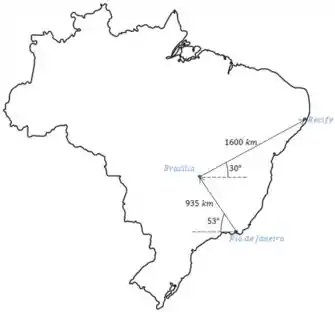
Um avião parte do Rio de Janeiro com destino a Recife, porém ele possui uma escala em Brasília. O primeiro trecho, entre Rio de Janeiro e Brasília, possui e o avião demora nele. Em seguida, o avião fica parado em Brasília por para abastecimento e embarque/desembarque de passageiros. O segundo trecho, entre Brasília e Recife, possui e o avião demora para percorrê-lo. A figura abaixo ilustra o plano de vôo do avião. Determine o módulo, direção e sentido da velocidade vetorial média do avião do inicio do vôo, no Rio de Janeiro, até o fim do vôo, no Recife. Considerando como a origem do sistema cartesiano a cidade do Rio de Janeiro.
Dados: , ,,
OBS: Pegue uma calculadora, você vai precisar !!!
Passo 1
Para calcular a velocidade média vetorial, devemos ter o deslocamento vetorial e o tempo total do percurso. Para isso devemos descobrir o deslocamento vetorial em cada trecho da viagem.
Vamos chamar de trecho 1 a parte Rio - Brasília e de trecho 2 a parte Brasília - Recife.
Passo 2
Primeiro vamos calcular o tempo total do percurso. Ele é a soma do tempo de vôo de cada trecho mais o tempo parado em Brasília.
Passo 3
Vamos achar agora os deslocamentos do trecho Rio – Brasília.
Para isso devemos decompor o vetor deslocamento entre as cidades, da mesma forma que fizemos no capítulo de vetores, atento ao sinal.
Usando a “regra do COlado/SEparado” teremos
.
Lembrando que para cima/para direita significa sinal positivo, enquanto para baixo/para esquerda significa sinal negativo.
Passo 4
Vamos achar agora os deslocamentos do trecho Brasília – Recife, da mesma forma que fizemos para o outro trecho.
Usando a “regra do COlado/SEparado” teremos.
Lembrando que para cima/para direita significa sinal positivo, enquanto para baixo/para esquerda significa sinal negativo.
Passo 5
Vamos agora achar o deslocamento total em cada direção,
Podemos escrever esse deslocamento da seguinte forma vetorial
Passo 6
A velocidade média vetorial pode ser calculada pela fórmula.
Escrever a velocidade média vetorial como vetor mostra a direção e sentido. Porém não o módulo.
Passo 7
O módulo de será,