UFSCAR, Sem Campus, Física 1, AV1 - 2021.1 - Prof° Raphael Santarelli, Questão 4d
Uma partícula se move em uma trajetória circular horizontal no plano , com velocidade escalar constante. No instante , a partícula possui velocidade e aceleração no sentido positivo de . No instante , a partícula possui velocidade e aceleração no sentido positivo de . Considere a diferença é menor que um período de rotação.
Quais os vetores velocidade e aceleração no instante ?
Passo 1
Oiie, tudo certinho?
Temos aqui uma partícula se movendo em uma trajetória circular sobre o plano , o enunciado nos dá algumas informações sobre instantes da trajetória, como por exemplo, nos indica que no instante , a velocidade da partícula é tal que
da mesma forma, temos que em , a velocidade é tal que
O enunciado também nos dá informações sobre a direção da aceleração nestes dois instantes, no primeiro instante a aceleração está no sentido positivo de , e no segundo instante, está no sentido positivo de . Por último, nos é afirmado que , em que é um período de rotação! Belezinha?
Queremos encontrar os vetores velocidade e aceleração no instante , o segredo para isso é encontrar a posição angular da partícula neste instante de tempo e utilizar esta informação para calcular as componentes dos vetores! Lembre que já sabemos os módulos de ambos, já que os dois têm módulo constante! Bora lá
Passo 2
Como temos que a velocidade escalar é constante, a posição angular da partícula ao longo da circunferência pode ser calculada através da expressão
Simplesmente para utilizar diretamente os dados que nos foram dados, vamos usar , ou seja, . E, a expressão acima toma a forma
Uma relação de proporcionalidade entre o ângulo em todo instante de tempo, vamos ter que encontrar a velocidade angular , isso é simples, já que podemos usar a relação
usando que e que , temos que a velocidade angular é
Ou seja, temos que para todo instante de tempo, nosso ângulo será dado por
Vamos usar essa expressão para encontrar o nosso ângulo no instante pedido e então trabalhar em obter o nosso vetor velocidade!
Passo 3
Em , temos que nosso ângulo será
mas como isso nos ajuda? Temos que em graus, este ângulo é dado por
ou seja, esquematicamente, temos que o vetor está aproximadamente na seguinte posição
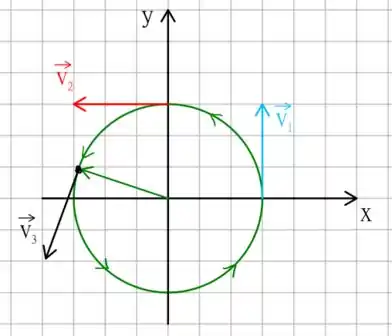
Mas, antes disso vamos olhar um pouco aos vetores e , podemos parametrizar os vetores velocidades tangencialmente em termos do ângulo se considerarmos a seguinte relação
Teste e na expressão acima se estiver com dificuldade de visualizar! Usando o ângulo que calculamos temos que
e, portanto, o nosso vetor é tal que
Vamos encontrar agora a nossa aceleração! Vem comigo!
Passo 4
Nós encontramos o vetor aceleração centrípeta em termos de uma direção arbitrária nas alternativas anteriores, temos que
No entanto, queremos escrever o vetor em termos das direções e , analisando a posição de nosso vetor no esquema realizado acima, temos que
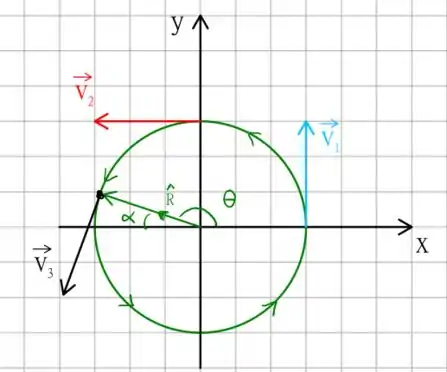
Vamos utilizar o ângulo , para calcular as componentes de como
usando que , temos que , portanto, temos que
e, portanto, o vetor aceleração é simplesmente
Uff… A questão foi isso! Te vejo na próxima! Tchauzinho!
Resposta
e