Desde janeiro até final de abril de , cerca de da população brasileira contraiu o vírus da dengue (fonte: Boletim Epidemiológico da Secretaria de Vigilância em Saúde – Ministério da Saúde, vol., n., ).
Suponha que um teste sanguíneo para detectar o vírus da dente seja tal que, dado que as pessoas contraíram o vírus, dê resultado positivo em dos casos, e dado que as pessoas não contraíram o vírus, dê negativo em dos casos. Suponha que uma pessoa faz o teste e o resultado dá positivo. Qual a probabilidade desta pessoa ter de fato o vírus da dengue?
Passo 1
Eaí gente bonita, tudo tranquilo?
Essa questão traz um contexto até interessante sobre a contaminação do vírus da dengue e a porcentagem de acerto dos exames. Mas, basicamente, a questão nos traz três informações:
1) As pessoas que contraíram o vírus e realizam o exame, recebem resultado positivo das vezes.
As pessoas que não contraíram, recebem negativo das vezes.
da população brasileira contraiu o vírus da dengue.
O enunciado nos pede para calcular a probabilidade de uma pessoa realmente ter o vírus da dengue, dado que o resultado do exame deu positivo.

Então galera, essas questões que trazem afirmações, diferentes possibilidades e etc, tem a cara da árvore de probabilidade. Sendo assim, vamos interpretar cada uma das afirmações usando a árvore, e em seguida calculamos o que foi pedido pelo exercício.
Vamo simbora?!
Passo 2
Bom, a primeira afirmação diz que as pessoas que contraíram o vírus e realizam o exame, recebem resultado positivo das vezes.
Ou seja, temos o universo das pessoas que contraíram o vírus da dengue e realizaram o exame. Daí, saem dois ramos:
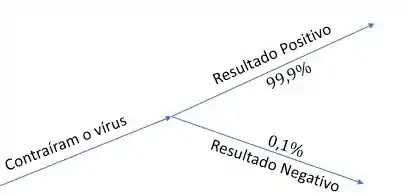
Massa!
A outra informação é que as pessoas que não contraíram, recebem negativo das vezes. Ou seja, temos um braço com as pessoas que não contraíram o vírus, e daí saem dois ramos também.
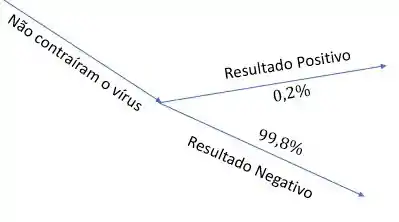
Boaa! Mas, pra usar a árvore precisamos juntar esses dois ramos. Aqui que entra a informação: da população brasileira contraiu o vírus da dengue. Assim:
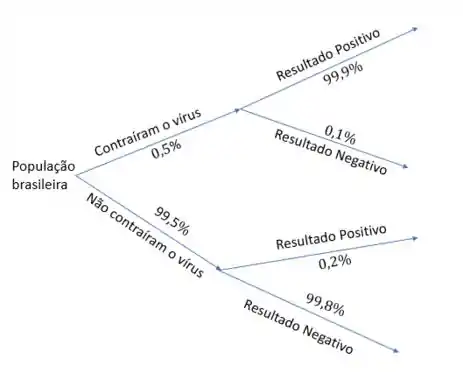
Excelente! Conseguimos montar a nossa árvore!
Passo 3
Agora vamos usar a nossa árvore de probabilidades para calcular o que foi pedido. Segundo o enunciado, devemos calcular a probabilidade de uma pessoa realmente ter o vírus da dengue, dado que o resultado do exame deu positivo.
Ou seja, uma probabilidade condicional. Lembra que:
Sendo o conjunto de pessoas cujo resultado do exame deu positivo, e o conjunto cujo resultado deu positivo e que também contraiu a doença.
Usando a nossa árvore, basta multiplicar as probabilidades pelo caminho até chegar aos ramos que nos interessam. Assim:
Já para , temos:
A unidade é como se fosse , mas como iremos fazer uma razão devido à probabilidade condicional, não precisamos nos preocupar com ela.
Fazendo:
Temos:
Portanto, a probabilidade pedida, vale:
ou
Prontinho gente, terminamos. Curtiram a solução?
Responde Aí!