Responda:
- Um dominó tem diferentes peças. De quantas formas podemos distribuir em cada uma de caixas iguais, deixando fora?
- De quantas formas podemos ordenar casais numa ciranda com os casais de mãos dadas?
- De quantas maneiras podemos ordenar os símbolos: a, a, b, b, c, d, e; sem que letras iguais fiquem vizinhas?
- De quantas maneiras podemos ordenar as letras de “ESCOLHA” se as vogais continuam ocupando as posições 1ª, 4ª e 7ª, e cada consoante não deve ocupar o lugar original?
Passo 1
Fala aí, gente, vamos começar pela letra “a” que nos pede para organizar peças em caixas iguais de peças e deixar de fora. Bom, como temos que organizar, mas não importa a ordem, podemos usar a Combinação que segue a fórmula:
Onde é o número de peças que queremos organizar, enquanto é o número de espaços que temos para organizar.
Considerando a organização da primeira caixa, nós temos o 6 vagas dentro da caixa e peças possíveis, logo nosso número de combinações possíveis é:
Agora pensando na segunda caixa que temos para organizar, não temos mais peças disponíveis, pois usamos na primeira caixa, logo teremos:
E nossa combinação para a segunda caixa será:
Faremos o mesmo pensamento para a terceira caixa:
Então o número de combinações possíveis para a terceira caixa é:
E por último, a última caixa terá:
Então o número de combinações possíveis para a quarta caixa é:
Vamos juntar todas essas possibilidades em uma única para organizar as caixas:
Como temos caixas e a organização delas não considera a ordem, então inserimos o fator de correção:
Nossa contagem de possibilidades no total é:
Substituindo os valores:
Simplificando essa conta:
Esse número é grande demais, então vamos deixar dessa forma mesmo!
Passo 2
Bom pessoal, a letra “b” pediu pra organizarmos uma ciranda com casais, se você é muito novo, talvez não saiba que ciranda é uma roda! Sim, a pessoa que vos fala é uma pessoa cringe.
Mas após essa informação que os casais estão organizados em uma roda, podemos usar a famosa Permutação Circular:
No nosso caso, como temos casais:
Mas calma lá, meu jovem gafanhoto, também temos que considerar que existem duas formas de cada casal se organizar, concorda? O primeiro par do casal pode estar do lado direito de seu parceiro ou do lado esquerdo, por esse motivo, temos que incluir em nossas possibilidades o fator:
Logo, o número de possibilidades é:
Resolvendo esse cálculo, temos:
possibilidades de organização!
Passo 3
A letra “c” quer organizar as letras quando temos repetição de letras e nós já sabemos que isso requer Permutação com repetição. Vamos supor inicialmente que podemos organizar de todas as formas possíveis, então só temos que considerar a fórmula com dois tipos de repetição:
Nós temos letras:
Então:
Mas a letra “a” se repete vezes:
Enquanto a letra “b” também se repete vezes:
Então se não ligarmos para a regra de organização, teremos um total de possibilidades de organização igual a:
Agora é hora de desconsiderar os casos que não queremos, ou seja, letras iguais como vizinhas, então vamos calcular quantas são essas possibilidades e subtrair depois.
Se considerarmos as letras “a” como um bloquinho lado a lado, teremos a permutação de elementos com uma repetição que será a letra “b”:
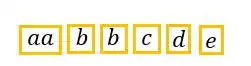
Logo usamos a fórmula:
Por outro lado, também podemos ter o mesmo caso considerando os b’s como vizinhos:

Teremos a permutação de elementos com uma repetição que será a letra “a”:
Pensa comigo que se vamos tirar todos os casos em que os a’s estão lado a lado e também vamos tirar todos os casos que os b’s estão lado a lado, então estamos tirando vezes que ocorre tanto os a’s e os b’s estarem lado a lado.
Se tanto os a’s são vizinhos e os b’s são vizinhos, então temos a permutação de apenas elementos:
Então nossa permutação se torna:
Agora é hora de somar e subtrair essas possibilidades:
Substituindo os valores que calculamos:
Calculando isso, ficamos com:
Logo, temos possibilidades!
Passo 4
Por último e não menos importante, nós temos a letra “d” que nos pede: De quantas maneiras podemos ordenar as letras de “ESCOLHA” se as vogais continuam ocupando as posições 1ª, 4ª e 7ª, e cada consoante não deve ocupar o lugar original.
Vamos nos atentar que ele fala que o que podemos mudar de lugar que são as consoantes, elas não devem ficar nos locais originais, então temos uma Permutação caótica. A permutação caótica é dada pela fórmula:
No nosso caso, como temos elementos que queremos escolher então, nossa permutação será:
Como temos possibilidades de letras para cada uma das vagas, então temos que corrigir esse número de possibilidades total:
Colocando o valor que encontramos para a permutação caótica:
Fazendo essas contas:
Resposta
a)
b)
c)
d)