UFPE, 1Avaliação, 2018.2, 3a.
Enuncie e demonstre o Teorema das Diagonais.
Passo 1
E aiii, galerinhaa!! Nessa questão, precisamos relembrar alguns assuntos de análise combinatória para enunciar o Teorema das Diagonais. Ela é uma identidade que diz o seguinte:
"A soma dos elementos situados na mesma diagonal desde o elemento da 1ª coluna até o de uma qualquer é igual ao elemento imediatamente abaixo deste."
Escrevendo pela notação dos binomiais, temos:
Passo 2
É muito fácil de entendermos a relação de Stifel quando lembramos da torre de Pascal. Vamos pensar um pouquinho:
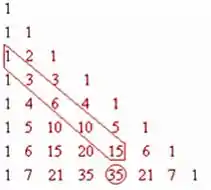
Agora conseguimos demonstrar o teorema!! Pelas propriedades dos binomiais, conseguimos começar a demonstração, relembrando a propriedade dos binomiais complementares:
A partir dela, temos:
Utilizando o Teorema das Colunas, temos também que:
E colocando no Teorema dos Binomiais novamente,
Assim, concluímos a justificativa do Teorema das Diagonais, como pedido:
E prontinho!!
Resposta
