UFPE, 1Avaliação, 2018.2, 3a.
Enuncie a relação de Stifel.
Passo 1
E aiii, galerinhaa!! Nessa questão, precisamos relembrar alguns assuntos de análise combinatória para enunciar a relação de Stifel. Ela é uma identidade que envolve coeficientes binomiais, e diz o seguinte:
"A soma de dois números binomiais de mesmo numerador e denominadores consecutivos é um número binomial cujo numerador possui uma unidade a mais que os numeradores das parcelas e o denominador é o maior dos denominadores das parcelas (Stifel, Michael)."
Passo 2
É muito fácil de entendermos a relação de Stifel quando lembramos da torre de Pascal. Vamos pensar um pouquinho:
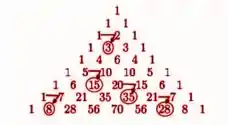
Se olharmos nas setinhas e nos círculos, veremos que todos os termos são a representação da soma dos dois números diferentes acima dele. E para representar isso matematicamente, nós temos a relação de Stifel, dada que, sejam os números naturais n e p em que n>= p-1 >= 0, é possível afirmar que:
Resposta
