Calcule a integral de linha do campo

Ao longo de uma curva fechada simples orientada positivamente e satisfazendo as duas seguintes propriedades:

1. O círculo de centro em e raio está no interior da região limitada pela curva ;
2. A área da região delimitada por é .

Agora vamos aplicar Green, mas com calma. Repare que temos uma singularidade no ponto (o denominador do campo dá zero), portanto, precisamos excluir ese ponto da região.

Bom como a questão fala que o círculo de centro em e raio está no interior da região limitada pela curva , poderíamos usar esse círculo para isolar o ponto (repare que o ponto está dentro dele). No entanto, isso pode não ser uma boa ideia por causa do denominador do campo: . Ia ser meio complicado de resolvermos essa integral de linha usando uma circunferência de raio !

Seria muito melhor se a gente isolasse esse ponto com a circunferência .

E nós podemos fazer isso, porque essa circunferência está dentro da cicunferência de raio centrada na origem, que o problema afirma estar dentro de . Portanto, a circunferência de raio deslocada também está dentro de ! Ficou confuso? Se liga nessa imagem:

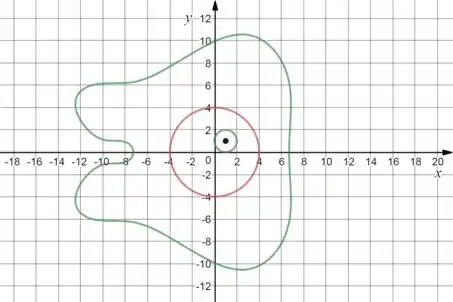
Imagina que a curva verde grande é a nossa curva que não conhecemos, então eu botei uma bem aleatória! A curva vermelha é a nossa circunferência de raio dentro de e a circunferência menorzinha verde é a curva que criamos para remover a singularidade (o pontinho preto).

Sendo, então, a região entre e essa circunferência verde e sendo orientada no sentido anti-horário e a circunferência horário, temos:

A questão também fala que a área da região delimitada por é . Podemos escrever então:

Como a circunferência tem raio , sua área é dada por :

Agora falta a integral na circunferência. Vamos parametrizá-la em coordenadas polares deslocadas com :

Como ela gira no sentido horário, vai de a . Agora derivamos isso aí:

Aplicamos a fórmula:

Lembrando que

Temos, então: