Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campos Singulares

Ver Teoria
Exercício 1512345678910111213141617181920212223242526272829303132333435363738

Enunciado

Seja

F → x , y = - y x 2 + y 2 , x x 2 + y 2 + x

Calcular a integral de linha vetorial ∫ C F → d r → , onde C é a curva união das curvas planas C 1 e C 2 :

C 1 é a fronteira do quadrado - 3,3 × - 3,3 orientada no sentido anti-horário

C 2 é a fronteira do quadrado 1 2 , 5 2 × - 1,1 orientado no sentido horário

Passo 1

Bom, o enunciado é bem grande, mas na verdade mesmo o que ele quer é a integral de linha

∫ C F → d r →

Onde C na verdade são duas curvas, então

∫ C F → d r → = ∫ C 1 F → d r → + ∫ C 2 F → d r →

Vai dar um trabalho tentar fazer isso da forma direta, não é? Até porque nosso campo é bem complicado também, vamos tentar usar o teorema de Green aqui!

A nossa curva C tem esse esboço aqui

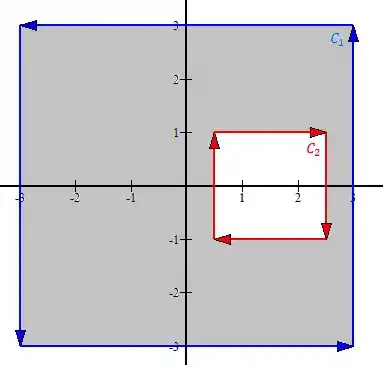
Perceba que já colocamos a região do teorema de Green aqui, nela percebemos um problema: o campo F → possui uma singularidade em 0,0 , porque o denominador fica zero! Então pra usar o teorema de Green aqui vamos ter que excluir esse ponto.

Beleza, mas qual a melhor curva pra excluir o ponto?

Bom, aqui vamos escolher uma circunferência α :   x 2 + y 2 = a 2 , onde 0 ≤ a ≤ 1 2 . Escolhemos essa curva porque o denominador do campo é exatamente x 2 + y 2 , então fica simples de calcular tudo depois.

Resumindo, o nosso novo esboço fica assim

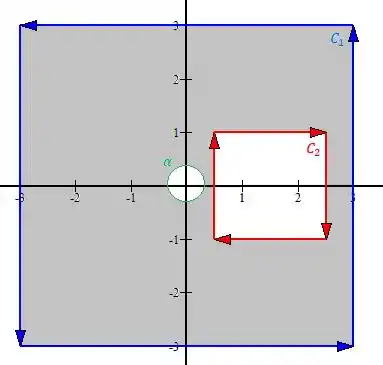
Note que excluímos a singularidade e, para isso, a orientação da curva α deve ser no sentido horário, nunca se esqueça de conferir a orientação da curva, ta bem?

O teorema de Green fica

∫ C F → d r → + ∫ α F → d r → = ∬ D ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Passo 2

Vamos começar calculando essa integral dupla do teorema. Pra isso precisamos derivar o campo F → .

F → = - y x 2 + y 2 , x x 2 + y 2 + x

∂ F 2 ∂ x = ∂ ∂ x x x 2 + y 2 + x

∂ F 2 ∂ x = x 2 + y 2 - 2 x 2 x 2 + y 2 2 + 1

∂ F 2 ∂ x = y 2 - x 2 x 2 + y 2 2 + 1

Agora derivando F 1

∂ F 1 ∂ y = ∂ ∂ y - y x 2 + y 2

∂ F 1 ∂ y = - x 2 + y 2 - 2 y - y x 2 + y 2 2

∂ F 1 ∂ y = y 2 - x 2 x 2 + y 2 2

Portanto a integral dupla fica

∬ D ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

= ∬ D y 2 - x 2 x 2 + y 2 2 + 1 - y 2 - x 2 x 2 + y 2 2 d A

= ∬ D 1 d A = Á r e a   d e   D

Bem mais fácil assim né? Bom, voltando pro nosso esboço, qual é a área de toda aquela região cinza?

A = A C 1 - A C 2 - A α

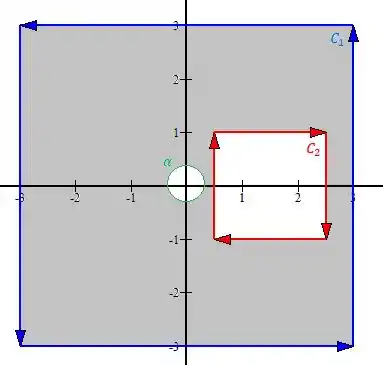
A área de C 1 é a área do quadrado de lado 6 , logo A C 1 = 36

A área de C 2 é a área do quadrado de lado 2, logo A C 2 = 4

A área de α é a área de um círculo de raio a , logo A α = π a 2

A = 36 - 4 - π a 2

A = 32 - π a 2

∬ D ∂ F 2 ∂ x - ∂ F 1 ∂ y d A = 32 - π a 2

Passo 3

Pra terminar a questão ainda falta calcular a integral da curva que acrescentamos, ou seja, a integral de α .

∫ α F → d r →

Pra isso precisamos parametrizar a curva. Como se trata de uma circunferência, temos

x = a cos ⁡ t

y = a sen ⁡ t

Onde

0 ≤ t ≤ 2 π

Só que queremos a orientação horária de t , certo? Então vamos inverter esses limites aí na integral, beleza?

Fazendo a integral de linha diretamente, precisamos derivar a parametrização da curva, lembra?

x ' = - a sen ⁡ t

y ' = a cos ⁡ t

d r → = - a sen ⁡ t , a cos ⁡ t d t

O campo F → fica assim

F → x , y = - y x 2 + y 2 , x x 2 + y 2 + x

F → = - a sen ⁡ t a 2 , a cos ⁡ t a 2 + a cos ⁡ t

F → = - sen ⁡ t a , cos ⁡ t a + a cos ⁡ t

Juntando tudo na integral

∫ α F → d r → = ∫ 2 π 0 - sen ⁡ t a , cos ⁡ t a + a cos ⁡ t . - a sen ⁡ t , a cos ⁡ t d t

= ∫ 2 π 0 sen 2 ⁡ t + cos 2 ⁡ t + a 2 cos 2 ⁡ t d t

= ∫ 2 π 0 1 + a 2 cos 2 ⁡ t d t

Pra integrar isso aí, sabemos que

cos 2 ⁡ t = 1 + cos ⁡ 2 t 2

Logo

∫ 2 π 0 1 + a 2 cos 2 ⁡ t d t = ∫ 2 π 0 1 + a 2 2 + a 2 cos ⁡ 2 t 2 d t

= t + a 2 2 t + a 2 sen ⁡ 2 t 4 2 π 0

= - 2 π - π a 2

Passo 4

Agora temos tudo, só juntar no teorema de Green lá do passo 1

∫ C F → d r → + ∫ α F → d r → = ∬ D ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

∫ C F → d r → - 2 π - π a 2 = 32 - π a 2

∫ C F → d r → = 32 + 2 π

Resposta

32 + 2 π

Exercícios de Livros Relacionados

7) Calcule oint_(gamma)^() - (y)/(x^2 + y^2) d x + (x)/(x^2 + y^2) d y onde γ é uma curva