Considere o campo vetorial dado por
- Mostre que , onde é a circunferência .
- O campo é conservativo em ? Justifique.
- Sendo , mostre que .
- Mostre que para toda curva fechada simples que circunde a origem.
Passo 1
Devemos então aqui calcular essa integral de linha pedida. Para fazer isso, temos dois possíveis métodos:
1º - Método direto.
2º - Teorema de Green.
Eu quero que você entenda do porquê vamos seguir o primeiro ao invés de usar o Teorema. Então venha comigo!
Passo 2
Se fôssemos utilizar o Teorema de Green, deveríamos antes de aplicar a igualdade de Green:
Verificar as condições do Teorema, que nos pede:
1º - Uma curva fechada delimitando uma região . O que não nos é um problema, afinal a curva é uma circunferência de certo raio (um número real).
2º - Orientada positivamente – girando no sentido anti-horário. O que também não é um problema, pois como o item não nos falou nada, tomamos como o sentido positivo esteja valendo.
3º - Um campo sem singularidades onde estamos trabalhando, e adivinha... Temos uma singularidade, afinal
Se substituíssemos as coordenadas da origem, teríamos uma divisão por zero o que sabemos ser impossível. Então temos uma singularidade na origem. E o que deveríamos fazer?
Eliminar o problema adicionando outra curva, uma circunferência, assim a região passaria a ser
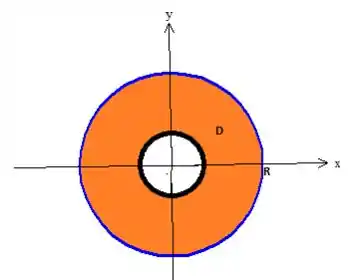
Mas repara que a integral de linha continuaria sendo calculada em cima de uma circunferência, logo, não há vantagens em resolver a integral pelo teorema, sacou?
Passo 3
Então vamos calcular a integral de linha de forma direta
Onde ...
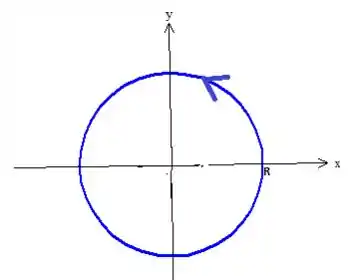
Precisamos primeiro parametrizar a curva:
Para fazer isso, basta usar as primas da mudança para as coordenadas polares...
Tome cuidado! não é variável como na mudança de coordenadas, e sim um número real ;).
O parâmetro dá uma volta completa
Passo 4
Com a parametrização em mãos, devemos substitui-la no termos do campo vetorial...
Substituindo pela parametrização (lembrando que )...
Passo 5
Prosseguindo, calculemos o termo :
Derivando...
Passo 6
Voltando para a integral de linha...
e substituindo tudo...
Lembrando que ...
Então é de fato válida a relação...
Passo 7
Existem várias formas de provar que a resposta para essa pergunta é não. O campo não é conservativo.
A forma mais fácil de provar isso é só observar que em um campo conservativo, em qualquer curva fechada pertencente ao domínio da função, o resultado da integral de linha é sempre zero.
Ora! Acabamos de calcular o resultado de uma integral de linha em cima de uma curva fechada e pertencente o domínio e o seu resultado foi diferente de , logo, o campo não é conservativo !
Passo 8
Nesse item basta calcular essas derivadas e verificar. Veja:
Fique atento a regra da cadeia...
Cuidado também com a regra da cadeia...
Calculando também a outra derivada...
Agora igualamos e vamos ver se de fato é igual ou não:
Para e diferente de ...
Epa!
Então de fato
Passo 9
Bem, qualquer curva que circunde o ponto . Como vimos lá atrás no passo , podemos calcular pelo teorema de Green, o resultado se eliminarmos o ponto , com uma circunferência:
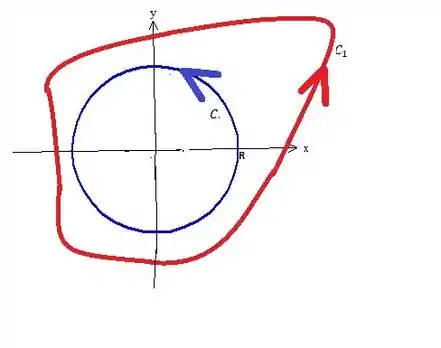
Pelo Teorema...
A integral de linha em Green é sempre calculada na borda da região , a borda é a curva bizarra e a curva ...
Podemos inverter esse sinal de menos se invertermos o sentido de giro da curva , ou seja, ao invés de girar para o sentido horário, girar no sentido anti-horário.
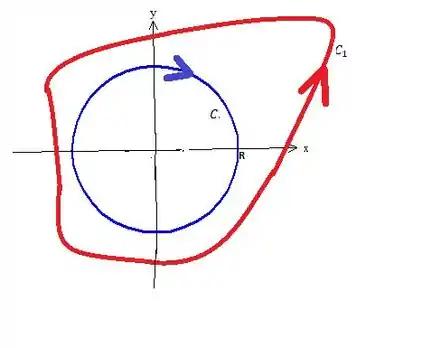
Já calculamos essa integral de linha, afinal é uma circunferência de raio qualquer, e o seu valor é...
Sacou?