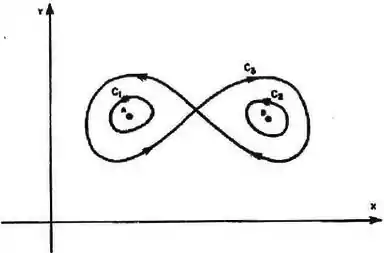
Sejam e funções reais de classe e ( e como na figura), tais que em . Sendo , , as curvas dadas na figura, calcule , supondo que:
Passo 1
O exercício nos pede pra calcular o integral de linha vetorial escrita na forma:
Mas não temos muita informação sobre o campo , apenas sobre as derivadas de suas componentes, .
Por sorte isso, isso já é o suficiente pra calcularmos o teorema de Green:
Até ai tudo bem, né? O problema é que a nossa curva não satisfaz as condições do teorema, porque não é simples e o campo não é definido em toda a região limitada pela curva por causa dos pontos e .
Mas calma que tem solução pra isso, vamos ver como fica!
Passo 2
Primeiro, vamos dividir a curva em dois pedaços, para garantir que, assim, teremos duas curvs simples. Dessa forma, vamos chamar de e (podemos ver que esse pedaço está no sentido horário e, portanto, botamos esse sinalzinho para identificar a orientação negativa) os pedaços:
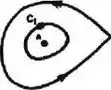
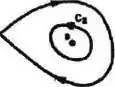
Agora sim temos duas curvas fechadas e simples, de forma que:
Agora só temos que resolver as singularidades.
Passo 3
Lembra que podemos criar curvas com “buracos” pra usarmos no teorema de Green?
Se fizermos então:
(Lembrando que as curvas internas devem ter orientação positiva, no sentido horário. E as curvas externas, orientação positiva, no sentido anti-horário.)
Com isso, temos que as regiões limitadas por e são válidas, então e , e podemos aplicar o teorema de Green:
E
Então vamos resolver uma por uma pra ver como que fica!
Passo 4
Na primeira, vamos ter:
Que é dado na questão, então:
Passo 5
Para a segunda, vamos ter:
Que também foi dado:
Passo 6
Por fim, vamos só jogar esses valores na integral que tinhamos lá em cima, vamos lembrar: