Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campos Singulares

Ver Teoria
Exercício 3012345678910111213141516171819202122232425262728293132333435363738

Enunciado

3) Calcule ∫ γ   F → d r → , onde γ t = cos ⁡ t , sin ⁡ t ,   t ∈ 0 ,   π e

F → x ,   y = - y x 2 + 4 y 2 + cos ⁡ y ,   x x 2 + 4 y 2 - x sin ⁡ y

Passo 1

Bem, antes da mais nada, separaremos essa função em duas...

F → = F → 1 + F → 2

Onde...

F → 1 = - y x 2 + 4 y 2 ,   x x 2 + 4 y 2                   e                 F → 2 = cos ⁡ y ,   - x sin ⁡ y

Então...

∫ γ   F → d r → = ∫ γ   F → 1 d r → + ∫ γ   F → 2 d r →

Passo 2

Primeiro vamos resolver o problema para ∫ γ   F → 2 d r → que parece ser menos chata...

Hmmmm, o problema até nos deu a curva já parametrizada, mas será que resolver a integral de linha ainda de uma forma direta seria uma boa?

A resposta é não. Afinal de contas, essa parametrização com essa parametrização ficaria um seno dentro de um próprio seno. Por isso, vamos buscar uma alternativa.

Essa alternativa é... O teorema de Green, afinal de contas...

∂ Q ∂ x - ∂ P ∂ y

Simplifica a nossa vida. Vamos calcula-lo?

F → 2 = P ,   Q = cos ⁡ y ,   - x sin ⁡ y

∂ Q ∂ x = - ∂ ∂ x x sin ⁡ y = - sin ⁡ y

∂ P ∂ y = + ∂ ∂ y cos ⁡ y = - sin ⁡ y

Logo...

∂ Q ∂ x - ∂ P ∂ y = 0

Olha que resultado bonito, senhoras e senhores! Indicando que sim, vamos usar o Teorema de Green! :D

Passo 3

O teorema de Green...

∫ ∂ D   F → d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A

Mas antes de aplicar a igualdade, devemos averiguar certas condições:

1º - Uma região D sendo delimitado pela superfície borda ∂ D .

2º - Um campo sem singularidades onde estamos trabalhando.

3º - Uma orientação positiva.

Passo 4

Infelizmente, caso desenhemos a curva γ t = cos ⁡ t , sin ⁡ t ,   t ∈ 0 ,   π , nos representa uma semicircunferência de raio 1 ...

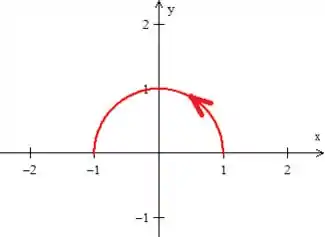
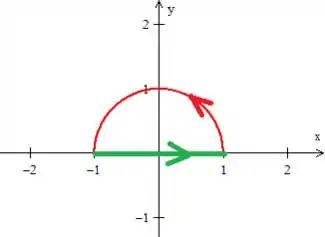
Como precisamos de uma região fechada, a fecharemos com uma reta y = 0 , que chamaremos de C 1 ...

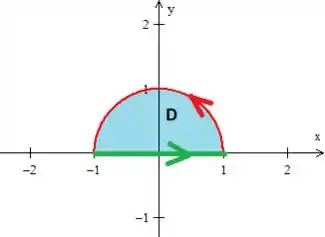
Esse campo F → 2 , não apresenta singularidades como uma divisão por 0 , ou algo do tipo.

Quanta a terceira condição, observe que elas estão orientadas no sentido positivo já que ambas giram no sentido anti-horário.

Logo, pelo Teorema...

∫ ∂ D   F → 2 d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A

Como a borda de D é C 1 e γ ...

∫ γ   F → 2 d r → + ∫ C 1   F → 2 d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A →

∫ γ   F → d r → + ∫ C 1   F → 2 d r → = 0 →

∫ γ   F → 2 d r → = - ∫ C 1   F → 2 d r →         →

Bora calcular essa integral?

Passo 5

Parametrizando a curva C 1 ...

γ 1 t = t ,   0

Onde t , vai de - 1 até 1 .

Calculando o termo d r → ...

d r → = 1 ,   0 d t

E substituindo no campo F 2 os termos da parametrização...

F → 2 = cos ⁡ y ,   - x sin ⁡ y

F → 2 γ 1 t = cos ⁡ 0 ,   - t sin ⁡ 0 = 1 ,   0

∫ C 1   F → 2 d r → = ∫ - 1 1 1 ,   0 ⋅ 1 ,   0 d t =

1 - - 1 = 2

Logo...

∫ γ   F → 2 d r → = - ∫ C 1   F → 2 d r → = - 2

Passo 6

Agora, vamos calcular a outra integral de linha

∫ γ   F → 1 d r →

Lembrando que chamamos de Q   e   P ...

F → 1 x ,   y = - y x 2 + 4 y 2 ⏟ P ,   x x 2 + 4 y 2 ⏟ Q

Vamos então calcular essa derivada de frações tomando cuidado na hora da regra da fração:

∂ Q ∂ x = ∂ ∂ x x x 2 + 4 y 2 = ∂ ∂ x x x 2 + 4 y 2

x 2 + 4 y 2 ∂ ∂ x x - x ∂ ∂ x x 2 + 4 y 2 x 2 + 4 y 2 2 =

x 2 + 4 y 2 - 2 x 2 x 2 + 4 y 2 2 =

- x 2 + 4 y 2 x 2 + 4 y 2 2

Calculando a outra...

∂ P ∂ y = ∂ ∂ y - y x 2 + 4 y 2 = ∂ ∂ y - y x 2 + 4 y 2 =

- x 2 + 4 y 2 ∂ ∂ y y + y ∂ ∂ y x 2 + 4 y 2 x 2 + 4 y 2 2 =

- x 2 + 4 y 2 + 8 y 2 x 2 + 4 y 2 2 =

- x 2 + 4 y 2 x 2 + 4 y 2 2

Então...

∂ Q ∂ x - ∂ P ∂ y = - x 2 + 4 y 2 x 2 + 4 y 2 2 - - x 2 + 4 y 2 x 2 + 4 y 2 2 =

0

Indicando que sim, vamos usar o Teorema de Green novamente! :D

Passo 7

Já sabemos que a curva é aberta e que precisamos fecha-la. Anteriormente, fechamos com uma reta, mas será que agora pode ser a reta?

Bem, vejamos a segunda condição: ela nos exige que tenhamos um campo sem singularidades onde estamos trabalhando...

F → x ,   y = - y x 2 + 4 y 2 + cos ⁡ y ,   x x 2 + 4 y 2 - x sin ⁡ y

Oh-ouh! O campo apresenta uma singularidade justamente em cima da reta que havíamos pegado, no 0 ,   0 . Por isso não a poderemos usar como curva novamente.

Vamos usar então a curva x 2 + 4 y 2 = 1 , pois ela simplifica o denominador, ao mesmo tempo ela pula o problema:

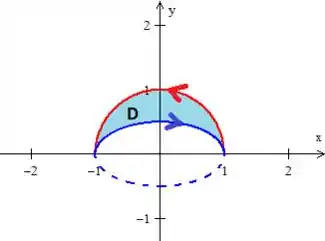
A chamaremos de C 2 . Observe que a borda de D é a curva γ e a curva C 2 ...

∫ ∂ D   F → 2 d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A   →

∫ γ   F → 2 d r → + ∫ C 2   F → 2 d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A

A última condição está sendo satisfeita, a final estão tudo girando no sentido anti-horário.

Passo 8

Aplicando então a igualdade a ferro e fogo...

∫ γ   F → 2 d r → + ∫ C 2   F → d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A   →

∫ γ   F → 2 d r → + ∫ C 2   F → 2 d r → = ∬ D   0 d A   →

∫ γ   F → 2 d r → = - ∫ C 2   F → 2 d r → →

Podemos mudar esse sinal menos se invertermos o sentido de giro da curva C , para - C (sentido anti-horário ou o oposto ao que já estava):

∫ γ   F → 2 d r → = ∫ - C 2   F → 2 d r →

Passo 9

Então calculemos a integral de linha...

∫ - C 2   F → 2 d r →

Primeiro parametrizando a curva - C ...

x 2 + 4 y 2 = 1

Comparando com cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ...

γ 2 θ = cos ⁡ θ , sin ⁡ θ 2

Enquanto θ dá uma meia volta...

0 ≤ θ ≤ π

Encontrando o termo d r → ...

d r → = γ 2 ' θ d θ

d r → = - sin ⁡ θ , cos ⁡ θ 2 d θ

Substituindo por fim a expressão de F → ...

F → 2 x ,   y = - y x 2 + 4 y 2 ,   x x 2 + 4 y 2   →

x 2 + 4 y 2 = 1

F → 2 γ 2 θ = - y ,   x →

F → 2 γ 2 θ = - sin ⁡ θ 2 ,   cos ⁡ θ

∫ - C 2   F → 2 d r → = ∫ 0 π - sin ⁡ θ 2 ,   cos ⁡ θ ⋅ - sin ⁡ θ , cos ⁡ θ 2 d θ =

∫ 0 π sin 2 ⁡ θ 2 + cos 2 ⁡ θ 2 d θ =

∫ 0 π 1 2 d θ = 1 2 π

Passo 10

Voltando para a integral geral...

∫ γ   F → d r → = ∫ γ   F → 1 d r → + ∫ γ   F → 2 d r →

∫ γ   F → d r → = - 2 + π 2

Resposta

- 2 + π 2

Exercícios de Livros Relacionados

7) Calcule oint_(gamma)^() - (y)/(x^2 + y^2) d x + (x)/(x^2 + y^2) d y onde γ é uma curva