Seja
um campo vetorial em . Calcule a integral de linha do campo ao longo da curva , orientada no sentido anti-horário, onde:
é a fronteira do retângulo .
Passo 1
Aqui vamos com calma. Antes de sair parametrizando e calculando a integral pela definição, vamos analisar o problema. Percebeu que parametrizar uma reta e substituir essa parametrização na expressão do campo vai dar algo bizarro, né?
Se você reparar, as componentes do campo são muito parecidas, o que significa que o seu rotacional pode ser zero. Se isso acontecer,nossa vida fica bem mellhor!
Lembrando que, em duas dimensões, o rotacional de um campo de resume a .
Bom, temos:
Pronto, provamos que o campo é conservativo.
Passo 2
Bem, se o campo é conservativo e a curva é fechada, quer dizer que a integral dá zero né? Não! Repare que temos um ponto não definido no campo: a origem .
Como esse ponto está dentro de não podemos simplesmente dizer que a integral dá zero: temos que remover esse ponto e aplicar o Teorema de Green.
Vamos isolar a origem com uma curva (que gira no sentido horário, para respeitar a orientação positiva). Nesse caso, pelo Teorema de Green, nós temos:
Ou seja, basta calcularmos a integral em para achar a integral em .
Mas quem nós vamos escolher para ser ? Olhando para a expressão do campo dá pra ver que ele implora pra gente escolher uma circunferência, né?
Vamos escolher como:
O que vai nos dar isso aqui:
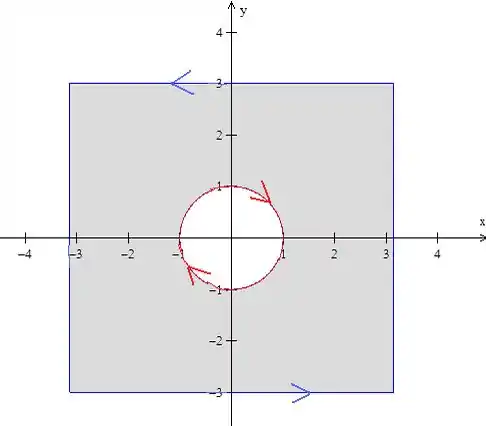
Passo 3
Bom, agora vamos parametrizar essa curva . Como se trata de uma circunferência, vamos usar coordenadas polares com :
Onde vai de a (porque o sentido é hórário).
Passo 4
Agora calculamos :
Passo 5
Vamos, então, usar a fórmula
O campo é dado por
Aplicando a parametrização, temos
Substituindo então na integral, temos
Passo 6
Finalmente, calculamos a integral
Passo 7
Logo