Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campos Singulares

Ver Teoria
Exercício 2712345678910111213141516171819202122232425262829303132333435363738

Enunciado

Questão 4: Calcule a integral de linha do campo vetorial

F x ,   y = - 2 y x 2 + y 2 4 + 2 x   ,   2 x x 2 + y 2 4 + x y + 1

Ao longo do círculo (circunferência) x 2 + y 2 = 1 orientado no sentido anti-horário.

Passo 1

Normalmente, podemos resolver integrais de linha de uma forma direta calculando essa integral:

∫ C   F x ,   y ⋅ d r →

Agora poxa! Você já deve ter notado que esse campo é muito complicado para trabalharmos com ele direto dessa forma, principalmente para integrar ao longo de uma circunferência .

Mas não se preocupe, pra isso que serve o teorema de Green:

∫ C   F x ,   y ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Ou seja, estamos prestes trocar essa integral de linha por uma integral dupla !

Passo 2

Mas se ainda estiver inseguro de aplicar Green, sugiro que calcule essa subtração de derivadas parciais, como vamos fazer agora:

F x ,   y = F 1 ,   F 2 = - 2 y x 2 + y 2 4 + 2 x   ,   2 x x 2 + y 2 4 + x y + 1

Derivando então...

∂ F 2 ∂ x = ∂ ∂ x 2 x x 2 + y 2 4 + x y + 1     →

∂ F 2 ∂ x = ∂ ∂ x 2 x x 2 + y 2 4 + y       →

∂ F 2 ∂ x = x 2 + y 2 4 ⋅ ∂ ∂ x 2 x - 2 x ⋅ ∂ ∂ x x 2 + y 2 4 x 2 + y 2 4 2 + y       →

∂ F 2 ∂ x = x 2 + y 2 4 ⋅ 2 - 2 x ⋅ 2 x x 2 + y 2 4 2 + y       →

∂ F 2 ∂ x = 2 x 2 + y 2 2 - 4 x 2 x 2 + y 2 4 2 + y       →

∂ F 2 ∂ x = y 2 2 - 2 x 2 x 2 + y 2 4 2 + y  

Calculando então a outra derivada parcial...

∂ F 1 ∂ y = ∂ ∂ y - 2 y x 2 + y 2 4 + 2 x           →

∂ F 1 ∂ y = x 2 + y 2 4 ⋅ ∂ ∂ y - 2 y - - 2 y ⋅ ∂ ∂ y x 2 + y 2 4 x 2 + y 2 4 2           →

∂ F 1 ∂ y = x 2 + y 2 4 ⋅ - 2 - - 2 y ⋅ y 2 x 2 + y 2 4 2           →

∂ F 1 ∂ y = - 2 x 2 - y 2 2 + y 2 x 2 + y 2 4 2           →

∂ F 1 ∂ y = - 2 x 2 + y 2 2 x 2 + y 2 4 2  

Então...

∂ F 2 ∂ x - ∂ F 1 ∂ y = y 2 2 - 2 x 2 x 2 + y 2 4 2 + y - - 2 x 2 + y 2 2 x 2 + y 2 4 2 =

y

POW! Que resultado, bonito, não é verdade. Isso é a prova “viva” que vamos utilizar mesmo o Teorema de Green, pois ele vai mesmo simplificar as nossas contas ;)

Passo 3

Bem, mas para aplicar o Teorema de Green precisamos no mínimo nos certificar se o teorema de fato pode ser aplicado, neh? Esse teorema, como já deve saber, exige três condições:

  1. Curva fechada C que delimita a região D .
  2. Sem singularidades onde estamos trabalhando.
  3. Curvas orientadas positivamente.

Vamos verificar cada uma a partir de agora, ok?

Passo 4

1 )

A começar pela primeira: uma curva fechada. Isso não é problema pra gente não é mesmo, já que estamos trabalhando em cima de uma circunferência (que delimita um círculo):

Passo 5

2 )

Agora na segunda condição do teorema, você vai entender o porquê de não usar essa região D : o campo F x ,   y não pode ter singularidades onde estamos trabalhando...

F x ,   y = - 2 y x 2 + y 2 4 + 2 x   ,   2 x x 2 + y 2 4 + x y + 1

E veja que ele tem um problema bem no ponto 0 ,   0 , pois se você substituir, cai em uma divisão por 0 ! Ou seja, o ponto do círculo que estávamos escolhendo está fora e isso não pode acontecer:

Então eis a pergunta: o que vamos fazer agora? Bem! Se não podemos utilizar o círculo, por causa de um ponto, vamos contornar esse ponto ! Tipo dessa forma aqui oh:

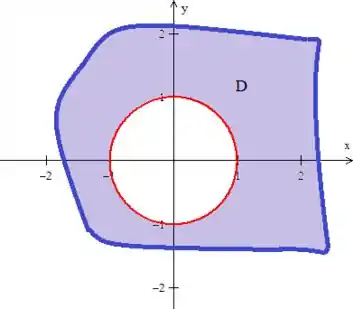
Veja que escolhemos uma curva qualquer e que está formando com a circunferência uma região fechada, o que é importante =)

Agora pera lá, não vamos usar uma curva qualquer, neh? Não! Vem comigo que eu te mostro como escolher a curva mais adequada .

Passo 6

Para a escolha da melhor curva, vamos sempre buscar simplificar mais a nossa vida, pra isso, dê uma olhada com atenção para o campo:

F x ,   y = - 2 y x 2 + y 2 4 + 2 x   ,   2 x x 2 + y 2 4 + x y + 1

Veja que o denominador dele seria algo interessante se simplificarmos, neh, substituindo por 1 , por exemplo:

x 2 + y 2 4 = 1

OPA!!! Essa equação, se você se recordar, é uma elipse!

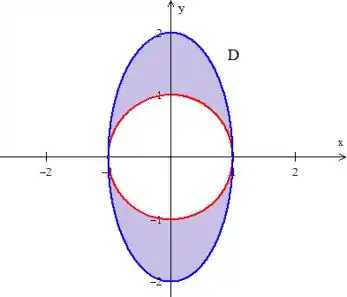
E o que é mais interessante, escolhendo essa elipse, depois o denominador do campo vai simplificar ! Sacou como podemos fazer a escolha perfeita?

Passo 7

3 )

Bem, mas não podemos nos esquecer, com isso tudo, de verificar a terceira condição de Green:

  1. Curvas orientadas positivamente.

Isso significa que a curva mais externa tem que estar girando no sentido anti-horário, enquanto todas as do interior, no sentido contrário (horário):

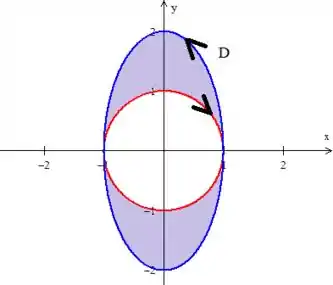
Passo 8

Finalmente, depois dessa análise toda, podemos aplicar o Teorema de Green:

∫ C   F x ,   y ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Agora tomando um cuidado, pois a curva C deve ser toda a curva que delimita a região D , ou seja:

C = C 1 ∪ C 2

∫ C 1   F x ,   y ⋅ d r → + ∫ C 2   F x ,   y ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Então se quisemos calcular a integral em cima da circunferência ( C 1 ) , como o enunciado nos pediu, podemos isolar...

∫ C 1   F x ,   y ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A - ∫ C 2   F x ,   y ⋅ d r →

Outra coisa que podemos fazer também, é que se você percebeu, essa circunferência está girando no sentido horário por exigência de Green, mas o que o problema realmente quer é que ela gire no sentido anti-horário. Isso pode ser concertado multiplicando tudo por - 1 :

- ∫ C 1   F x ,   y ⋅ d r → = - ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A + ∫ C 2   F x ,   y ⋅ d r →             →

∫ - C 1   F x ,   y ⋅ d r → = - ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A + ∫ C 2   F x ,   y ⋅ d r →  

Veja que aquele menos na frente da integral de linha foi parar em... - C 1 . Esse menos na frente de C 1 significa que ele mudou o sentido, ou seja:

Sentido Horário → Sentido Anti-horário

Que a gente quer, neh?

Passo 9

Então vamos calcular integral por integral, então.

A começar aqui pela integral dupla:

∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A = ∬ D   y   d A

Veja que a gente poderia até calcular essa integral dupla da forma tradicional: descrevendo a região D e integrando. Mas seria um grande trabalho e existe um bizu, quando se pega integrais duplas de y sozinho ou de x : verificar se a região tem simetria!

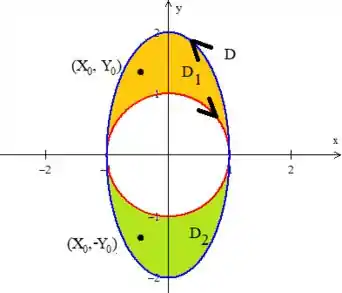
Pelo desenho, se pode notar que a região tem simetria com relação ao eixo x (A parte de cima se parece com a parte de baixo).

Se calcularmos a função y em cima do ponto x 0 ,   y 0 , vamos obter o valor de y 0 . Já se calcularmos o y no simétrico x 0 ,   - y 0 , vamos obter - y 0 . Como integral de y é uma “Soma” dos valores de y em todos os pontos, podemos pensar que os valores calculados na região de cima, vão se anular com os valores calculados na de baixo, saca?

Matematicamente falando... Se você calcular a integral de y na região de cima, você vai encontrar um valor...

∬ D 1   y d A

Já se você integrar na parte de baixo...

∬ D 2   - y d A

Como as regiões D 1 e D 2 são simétricas... A integral na região toda...

∬ D   y d A = ∬ D 1   y d A + ∬ D 2   - y d A = 0

Agora, isso só é valido, se as regiões D 1 e D 2 , forem realmente simétricas, e existe uma forma de provar isso: Vamos pegar as fronteiras:

C 1 = :             x 2 + y 2 = 1

C 2 = :             x 2 + y 2 4 = 1

Se substituirmos o ponto x 0 ,   y 0 ou x 0 ,   - y 0 , vamos encontrar o mesmo valor em cada uma delas, provando a simetria com relação ao eixo x ...

x 0 2 + - y 0 2 = 1       →           x 0 2 + y 0 2 = 1

O mesmo acontece com a outra !

Passo 10

Vamos agora calcular a integral de linha que ficou pra trás:

∫ C 2   F x ,   y ⋅ d r →

  • Primeiro parametrizando C 2 ...

    •   x 2 + y 2 4 = 1       →           x 2 1 2 + y 2 2 2 = 1      

    Como é uma elipse, podemos parametrizar com as primas das coordenadas polares...

    x = cos ⁡ θ

    y = 2 sin ⁡ θ

    Logo... ( θ dá uma volta completa para formar a elipse)

    r → θ = cos ⁡ θ ,   2 sin ⁡ θ ,       θ ∈ 0 ,   2 π

  • Agora calculando d r → ...

    • d r → = r ' θ d θ           →                 d r → = - sin ⁡ θ ,   2 cos ⁡ θ d θ

  • Por fim, substituindo os termos da parametrização em F x ,   y ...

F x ,   y = - 2 y x 2 + y 2 4 + 2 x   ,   2 x x 2 + y 2 4 + x y + 1     →

F x ,   y = - 2 2 sin ⁡ θ 1 + 2 cos ⁡ θ   ,   2 cos ⁡ θ 1 + cos ⁡ θ 2 sin ⁡ θ + 1   →

F x ,   y = - 4 sin ⁡ θ + 2 cos ⁡ θ   ,   2 cos ⁡ θ + 2 cos ⁡ θ sin ⁡ θ + 1

Substituindo o resultado dos três pontos na integral de linha...

∫ C 2   F x ,   y ⋅ d r → = ∫ 0 2 π - 4 sin ⁡ θ + 2 cos ⁡ θ   ,   2 cos ⁡ θ + 2 cos ⁡ θ sin ⁡ θ + 1 ⋅ - sin ⁡ θ ,   2 cos ⁡ θ d θ =

∫ 0 2 π 4 sin 2 ⁡ θ - 2 sin ⁡ θ cos ⁡ θ + 4 cos 2 ⁡ θ + 4 cos 2 ⁡ θ sin ⁡ θ + 2 cos ⁡ θ d θ =

∫ 0 2 π - 2 sin ⁡ θ cos ⁡ θ + 4 cos 2 ⁡ θ sin ⁡ θ + 2 cos ⁡ θ + 4 d θ =

Integrando...

cos 2 ⁡ θ - 4 cos 3 ⁡ θ 3 + 2 sin ⁡ θ + 4 θ 0 2 π = 8 π

Passo 11

Voltando, finalmente, para o teorema de Green...

∫ - C 1   F x ,   y ⋅ d r → = - ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A + ∫ C 2   F x ,   y ⋅ d r →  

E substituindo os resultados...

∫ - C 1   F x ,   y ⋅ d r → = 0 + 8 π  

∫ - C 1   F x ,   y ⋅ d r → = 8 π

Resposta

8 π

Exercícios de Livros Relacionados

7) Calcule oint_(gamma)^() - (y)/(x^2 + y^2) d x + (x)/(x^2 + y^2) d y onde γ é uma curva