Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campos Singulares

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829303132333435363738

Enunciado

3) Seja

G x ,   y = y 2 2 - y x 2 + y 2 + x e x 2 + y 2 ,   y e x 2 + y 2 + x x 2 + y 2

um campo de classe C 1 em R 2 \ 0 ,   0 . Seja C a curva dada pela concatenação do segmento que une 1 ,   0 a 2 ,   0 , o arco da circunferência com centro na origem, sentido anti-horário, indo de 2 ,   0 a - 2 ,   0 e o segmento que une - 2 ,   0 a - 1 ,   0 .

Calcule

∫ C   G → ⋅ d r →

Sugestão: Construa uma curva β que “feche” a curva C adequadamente, de modo que seja possível usar o Teorema de Green na região D que tem a curva fechada como fronteira.

Passo 1

Bem, como o próprio problema nos sugeriu, vamos mata-lo utilizando o Teorema de Green, afinal o campo é extremamente complexo e chato e curva C ... Nem precisa falar nada neh? Pelo Teorema de Green...

∫ C   G → ⋅ d r → = ∬ D   ∂ G 2 ∂ x - ∂ G 1 ∂ y d V

Bem, mas aí surgem algumas dúvidas, neh?

1º - Quem é a curva C e quem é a região D que tem essa C como borda?

2º - será que estamos nas condições de aplicar o Teorema?

3º - E por último, qual é o resultado dessa subtração de derivadas parciais?

Vamos descobrir! :D

Passo 2

Em relação a primeira pergunta, sobre quem é a “linha” C , não há muito mistério. Basta pegar as dicas que o problema deu e ir construindo essa curva:

1º - Um segmento de reta indo de 1 ,   0 a 2 ,   0 .

2º - Uma semicircunferência indo de 2 ,   0 até - 2 ,   0 .

3º - Por fim, outro segmento indo de - 2 ,   0 a - 1 ,   0 :

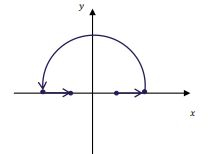
Sacou? Mais observe que essa curva C , está aberta, e sabemos muito bem que para aplicar o Teorema de Green, temos que ter uma curva fechada delimitando a região D . Ora bolas, como a própria dica nos falou, vamos fechar a curva C com uma outra curva!

Normalmente fecharíamos C , com um outro segmento de reta...

Maaaassss, temos um problema...

Passo 3

O problema que é justamente na 3º indagação láaaa no início. Será que estamos nas condições do Teorema de Green? E a resposta é não.

Para começar, Green nos exige uma curva fechada, e não temos. Segundo, a região fechada, inclusive as curvas, não pode conter singularidades do campo.

G x ,   y = y 2 2 - y x 2 + y 2 + x e x 2 + y 2 ,   y e x 2 + y 2 + x x 2 + y 2

Veja que se substituirmos x = 0 e y = 0 na função, ganhamos uma divisão por 0 o que sabemos ser impossível. Então o campo não está definido na origem. Por isso que não podemos pegar esse segmento de reta que passa pela origem.

Qual é a ideia, é justamente fechar com outra curva... No caso outro pedaço de circunferência:

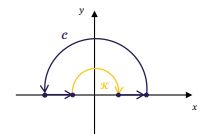
Passo 4

Uma semicircunferência de raio 1 que vamos chamar de C 2 , entrou na brincadeira e já está delimitando uma região D junto com a curva C :

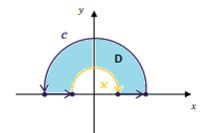
Note que a última condição de Green que não falamos foi sobre o sentido de giro que deve estar orientado positivamente. Como elas já estão girando no sentido anti-horário... Tá tudo certo e podemos aplicar a igualdade:

∫ ∂ D   G → ⋅ d r → = ∬ D   ∂ G 2 ∂ x - ∂ G 1 ∂ y d V

Repare que integral de linha de Green, é sempre calculada em cima da curva fechada ∂ D que é a borda de D . Essa borda no nosso caso, nada mais é do que C e C 2 ...

∫ C   G → ⋅ d r → + ∫ C 2   G → ⋅ d r → = ∬ D   ∂ G 2 ∂ x - ∂ G 1 ∂ y d V

Se queremos a integral de linha em   C , isolemos a integral ...

∫ C   G → ⋅ d r → = ∬ D   ∂ G 2 ∂ x - ∂ G 1 ∂ y d V - ∫ C 2   G → ⋅ d r →

Ainda podemos simplificar um pouco mais, se trocarmos aquele sinal de menos ali, invertendo o sentido de giro de C 2 ...

∫ C   G → ⋅ d r → = ∬ D   ∂ G 2 ∂ x - ∂ G 1 ∂ y d V + ∫ - C 2   G → ⋅ d r →

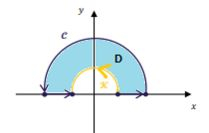
A principio nem parece que simplificou tanto, mas trabalhar com ela girando no sentido anti-horário... Sim é menos chato ;)

Passo 5

Vamos calcular a integral dupla primeiro. Repare que ainda não respondemos a última pergunta dada lá no início. A respeito da subtração de derivadas parciais. Cara, não tem muito segredo! Basta pegar o campo e derivar...

G x ,   y = y 2 2 - y x 2 + y 2 + x e x 2 + y 2 ⏟ G 1 ,   y e x 2 + y 2 + x x 2 + y 2 ⏟ G 2

∂ G 2 ∂ x = ∂ ∂ x y e x 2 + y 2 + x x 2 + y 2

∂ G 2 ∂ x = ∂ ∂ x y e x 2 + y 2 + ∂ ∂ x x x 2 + y 2

É... Vai dar um certo trabalhinho calcular essas derivadas aí, mas vêm comigo na regra da cadeia da primeira...

∂ G 2 ∂ x = y e x 2 + y 2 ⋅ ∂ ∂ x x 2 + y 2 + ∂ ∂ x x x 2 + y 2   →

∂ G 2 ∂ x = 2 x y e x 2 + y 2 + ∂ ∂ x x x 2 + y 2   →

Derivando agora essa fração aplicando a regra da fração...

∂ G 2 ∂ x = 2 x y e x 2 + y 2 + x 2 + y 2 ∂ x ∂ x - x ∂ x 2 + y 2 ∂ x x 2 + y 2 2   →

∂ G 2 ∂ x = 2 x y e x 2 + y 2 + x 2 + y 2 - 2 x 2 x 2 + y 2 2  

∂ G 2 ∂ x = 2 x y e x 2 + y 2 + - x 2 + y 2 x 2 + y 2 2

Derivada a primeira! Agora calculemos a outra derivada da subtração...

∂ G 1 ∂ y = ∂ ∂ y y 2 2 - y x 2 + y 2 + x e x 2 + y 2   →

∂ G 1 ∂ y = ∂ ∂ y y 2 2 - ∂ ∂ y y x 2 + y 2 + ∂ ∂ y x e x 2 + y 2   →

Calculando essa primeira derivada...

∂ G 1 ∂ y = y - ∂ ∂ y y x 2 + y 2 + ∂ ∂ y x e x 2 + y 2   →

Essa segunda derivada aí... Seja esperto, não calcula tudo novamente não, vai dar o mesmo resultado, só que trocando x por y lá em cima...

∂ G 1 ∂ y = y - - y 2 + x 2 x 2 + y 2 2 + ∂ ∂ y x e x 2 + y 2

Sacou?

∂ G 1 ∂ y = y + y 2 - x 2 x 2 + y 2 2 + ∂ ∂ y x e x 2 + y 2

Calculando essa última derivada...

∂ G 1 ∂ y = y + y 2 - x 2 x 2 + y 2 2 + 2 x y e x 2 + y 2

Aplicando a subtração...

∂ G 2 ∂ x - ∂ G 1 ∂ y = 2 x y e x 2 + y 2 + - x 2 + y 2 x 2 + y 2 2 - y + y 2 - x 2 x 2 + y 2 2 + 2 x y e x 2 + y 2

∂ G 2 ∂ x - ∂ G 1 ∂ y = - y

Passo 6

Assim, a integral dupla fica sendo...

∬ D   ∂ G 2 ∂ x - ∂ G 1 ∂ y d V = ∬ D   - y   d V

A integral está sendo calculada em uma região D que é uma semicircunferência...

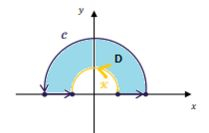
Logo... As coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

Para descobrir a variação de r e θ ... Olhemos novamente a região:

Repare que ela dá uma meia volta, portanto, θ ...

0 ≤ θ ≤ π

Enquanto isso, r ...

1 ≤ r ≤ 2

Substituindo na integral dupla...

∬ D   - y   d V = - ∫ 0 π ∫ 1 2 r sin ⁡ θ ⋅ J   d r d θ =

- ∫ 0 π ∫ 1 2 r 2 sin ⁡ θ   d r d θ

Resolvendo primeiro a integral de dentro...

- ∫ 0 π sin ⁡ θ ∫ 1 2 r 2   d r d θ =

- ∫ 0 π sin ⁡ θ r 3 3 1 2 d θ = - 8 3 - 1 3 ∫ 0 π sin ⁡ θ d θ =

- 7 3 - cos ⁡ θ 0 π =

- 7 3 - cos ⁡ π - - cos ⁡ 0 =

- 14 3

Passo 7

Calculando agora a integral de linha...

∫ - C 2   G → ⋅ d r →

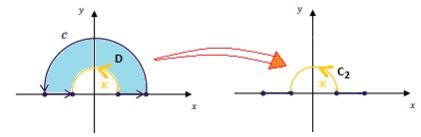
Precisamos da curva parametrizada...

x = cos ⁡ t

y = sin ⁡ t

Ou...

γ t = cos ⁡ t , sin ⁡ t

Onde t , dá uma meia volta...

0 ≤ t ≤ 2 π

Calculando agora o d r → ...

d r → = γ ' t d t

γ ' t = - sin ⁡ t , cos ⁡ t

Então, eis o d r → ...

d r → = - sin ⁡ t , cos ⁡ t   d t

Só nos falta agora mesmo substituir essa parametrização no campo G ... Lembre-se que x 2 + y 2 = 1 (raio da semicircunferência):

G x ,   y = y 2 2 - y x 2 + y 2 + x e x 2 + y 2 ,   y e x 2 + y 2 + x x 2 + y 2   →

G x ,   y = y 2 2 - y + x e 1 ,   y e 1 + x   →

G γ t = sin ⁡ t 2 2 - sin ⁡ t + e cos ⁡ t ,   e sin ⁡ t + cos ⁡ t   →

G γ t = sin 2 ⁡ t 2 - sin ⁡ t + e cos ⁡ t ,   e sin ⁡ t + cos ⁡ t

Passo 8

Substituindo na integral...

∫ - C 2   G → ⋅ d r → = ∫ 0 π sin 2 ⁡ t 2 - sin ⁡ t + e cos ⁡ t ,   e sin ⁡ t + cos ⁡ t ⋅ - sin ⁡ t , cos ⁡ t d t

∫ 0 π - sin 3 ⁡ t 2 + sin 2 ⁡ t - e sin ⁡ t cos ⁡ t + e sin ⁡ t cos ⁡ t + cos 2 ⁡ t d t =

∫ 0 π - sin 3 ⁡ t 2 + 1 d t =

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - ∫ 0 π sin 3 ⁡ t 2 d t + ∫ 0 π d t

A segunda integral é mole...

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - ∫ 0 π sin 3 ⁡ t 2 d t + t 0 π =

- 1 2 ∫ 0 π sin 3 ⁡ t d t + π

Essa outra integral aí, vamos fazer um trabalhinho com ela...

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - 1 2 ∫ 0 π sin 2 ⁡ t sin ⁡ t d t + π

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - 1 2 ∫ 0 π 1 - cos 2 ⁡ t sin ⁡ t d t + π

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - 1 2 ∫ 0 π sin ⁡ t - sin ⁡ t cos 2 ⁡ t d t + π

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = 1 2 ∫ 0 π - sin ⁡ t d t + 1 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t d t + π

Essa primeira integral aí, também é mole...

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = 1 2 cos ⁡ t 0 π + 1 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t d t + π

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = 1 2 cos ⁡ π - cos ⁡ 0 + 1 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t d t + π

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - 1 + 1 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t d t + π

Essa outra integral, podemos resolver fazendo uma substituição...

cos ⁡ t = a     →         d a = - sin ⁡ t d t

t = 0       →             a = cos ⁡ 0 = 1

t = π       →             a = cos ⁡ π = - 1

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - 1 + 1 2 ∫ 1 - 1 a 2 - d a + π

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - 1 + 1 2 ∫ - 1 1 a 2 d a + π

∫ 0 π - sin 3 ⁡ t 2 + 1 d t = - 1 + 1 2 a 3 3 - 1 1 + π =

= - 1 + 1 2 1 3 - - 1 3 3 + π =

- 1 + 1 3 + π = π - 2 3

Passo 9

Voltando ao Teorema de Green láaaa do passo 4 ...

∫ C   G → ⋅ d r → = ∬ D   ∂ G 2 ∂ x - ∂ G 1 ∂ y d V + ∫ - C 2   G → ⋅ d r →

E substituindo esses resultados...

∫ C   G → ⋅ d r → = - 14 3 + π - 2 3 =

- 16 3 + π

Resposta

- 16 3 + π

Exercícios de Livros Relacionados

7) Calcule oint_(gamma)^() - (y)/(x^2 + y^2) d x + (x)/(x^2 + y^2) d y onde γ é uma curva