Campos conservativos, Integrais de linha – caso vetorial, Teorema de Green
Calcule , onde é a curva dada por , , orientada de a .
Passo 1
Essa integral parece meio complicada de se calcular pela definição, não é? Parametrizar essa circunferência e depois aplicar isso na expressão do campo vai nos dar algo bizarro... Nem tente fazer isso!
Vamos, então, calcular o valor de para ver se conseguimos simplificar a questão. Temos:
Como
Ótimo, o campo é conservativo.
Passo 2
Sabemos que esse campo é conservativo, então, não precisamos calcular essa integral pela definição. Vamos, então, calcular a função potencial desse campo. Certo?
É... nesse caso tá meio difícil calcular a função potencial, né? Integrar não é muito simples
Então, vamos optar por outro caminho, vamos usar o Teorema de Green. Para isso, precisamos fechar nossa curva, não é? Temos um arco de circunferência que vai de até .
O mais natural e o mais simples é fechar com uma reta, que liga os pontos final de inicial. E quando resolvermos a integral de linha sobre a reta, vamos ter uma expressão relativamente simples.
Temos essa curva aqui então:
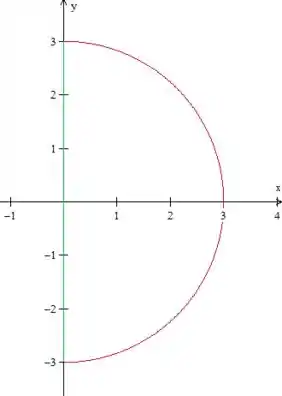
Certo? Senta aí que tem mais.
Temos que tomar cuidado com um detalhe: o campo tem uma indeterminação, não está definido no ponto , esse ponto faz o denominador da expressão do campo zerar. Então esse ponto não pode estar dentro da região limitada pela nossa curva. E adinha? Ele está -.-
Ferrou agora, né? Calma, vamos pensar um pouco.
Nós podemos isolar esse ponto, envolvendo ele por uma circunferência. Mas não qualquer circunferência, dá uma olhada na expressão do campo:
Ela está querendo nos dizer algo, né? Repare que o denominador é quase uma circunferência, só falta o “ ”. Então, vamos usar a circunferência para isolar o ponto. Por que? Porque isso vai simplificar muito nossa vida daqui a pouco, confia.
Beleza, então nossa região passa a ser essa aqui:
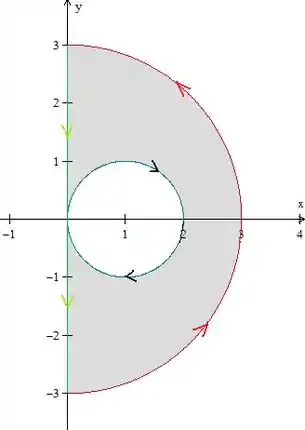
Repare que a curva toda está orientada positivamente, ou seja, caminhando pela curva, sempre vemos nossa região à esquerda.
Só cuidado com uma coisa: essa orientação da figura não é a mesma que o enunciado deu para , então essa curva que desenhamos , beleza? Temos então:
Onde é a reta e a circunferência que nós criamos. Logo, temos:
Beleza,? Vamos calcular essas integrais pela definição agora.
Passo 3
Precisamos agora parametrizar essas curvas que nós criamos.
Para a reta
Como é uma reta contida no eixo , podemos parametrizá-la assim:
Pois para qualquer , Pela figura, já vemos que vai de a (cuidado com o sentido da reta).
Para a circunferência
Nós criamos a seguinte circunferência , centrada em . Como se trata de uma circunferência, vamos usar coordenadas polares, certo?
Esse foi adicionado na definição de para cancelar o na equação da circunferência e, assim, manter a identidade .
Como temos , a parametrização fica:
Como temos uma volta completa, no sentido horário, vai de a .
Passo 4
Agora vamos derivar essa parametrizações:
Passo 5
Podemos, então, substituir os valores que encontramos na fórmula abaixo:
Para cada uma das curvas. Não se esqueça de escrever o campo
Em função das variáveis de cada parametrização.
Para a reta
Esse intervalo de integração é o mesmo que encontramos ao parametrizar a reta.
Para a circunferência
Para a outra integral, repare que substituindo a parametrização:
Na expressão do campo, temos:
Viu? Por esse motivo que era uma boa escolher essa cincunferência para isolar o ponto , porque, como a sua equação é extremamente parecida com o denominador da expressão do campo, substituindo a parametrização nele as coisas ficam muito mais simples!
A integral fica então:
Passo 6
Agora falta só resolver essa integrais que encontramos:
Lembrando que a integral de linha que o problema pede é dada por:
Temos