Considere o campo
com ∈ . Usando Green, resolva as seguintes questões:
a) Desenhe a região limitada por , e e selecione uma parametrização orientada positivamente para seu contorno (ou orientada anti-horáriamente).
b) Determine os valores do parâmetro a de modo que a integral .
c) Calcule a integral de linha do campo para o valor .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão foi dado um vetor com uma constante arbitrária onde
No item a) a questão apenas nos pede pra calcular uma região limitada pelas curvas , e e escrever como uma parametrização.
No item b) temos que descobrir um valor para a constante para satisfazer a integral .
E por último, no item c) vamos substituir por e calcular a integral .
E como podemos fazer esses cálculos?? 🤔
Perceba que temos uma integral do tipo , nesses casos, certamente temos que usar o Teorema de Green para nos ajudar, até porque seria muito difícil calcular uma integral para nesse caso.
Entendeu? Bora lá! 🐱👤
Passo 2
Vamos começar desenhando a região . Plotando as curvas , e , vamos obter a seguinte região.
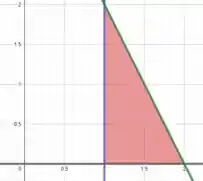
Se a gente usar como e como , vemos que deve ser maior que e menor que e deve ser maior que e menor que , ou seja, a parametrização para essa curva é
Certinho essa parte? 😉
Agora no item b) vamos obter um valor para tal que .
Para essa condição ser satisfeita, temos que ter , se pelo vetor , e , vamos aplicar essas derivadas.
Derivando em função de
Por derivação polinomial, temos
Tranquilo até aqui? 😁
Passo 3
Agora derivamos com relação a
Também pelo método de integração polinomial
Forçando , temos
Simplificando a equação
Ou seja, dizemos que se o campo é conservativo e para isso acontecer deve ser !
Bacana, não é? 😉
Por fim, vamos obter a integral
Para .
Pelo Teorema de Green, podemos escrever
Vimos que resulta em uma função bem pequena, então vamos calcular pelo segundo modelo.
Substituindo por , temos
Está acompanhando?
Passo 4
Como já parametrizamos , vamos substituir por na nossa função de integração e aplicando os limites de integração de acordo com o intervalo obtido no item a), temos
Aplicando o método de integração polinomial
Aplicando os limites de integração
Simplificando o resultado, temos
Agora com base nesse resultado integramos com relação a
Aplicando os limites de integração
Portanto o resultado da integral que procurávamos, é
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
a)
b)
c)