Seja
Calcule onde é a curva , orientada no sentido anti-horário.
Passo 1
Bom, já deu para ver que calcular essa integral aí pela definição deve dar muito trabalho, né? Vamos tentar aplicar Green então. Temos:
Bom, isso quer dizer que o campo é conservativo.
Passo 2
Pelo Teorema de Green, considerando uma curva fechada orientada no sentido anti-horário e a região limitada por ela, temos:
Ok, agora vamos analisar nossa curva :
Isso é uma elipse, certo? Portanto uma curva fechada. Então, vamos aplicar Green em !
Pera aí, olha a expresão do campo:
Temos uma singularidade no ponto , onde o denominador dessas frações é zero, portanto, a região onde vamos aplicar Green não pode conter a origem.
Já que a origem está dentro da elipse , precisamos excluir esse ponto da região o envolvendo com uma outra curva.
Para facilitar as contas, vamos usar a elipse:
Pois sua equação tem muita semelhança com o denominador do campo (isso vai simplificar as coisas).
Ok, então a fronteira em que vamos aplicar Green é essa aqui:
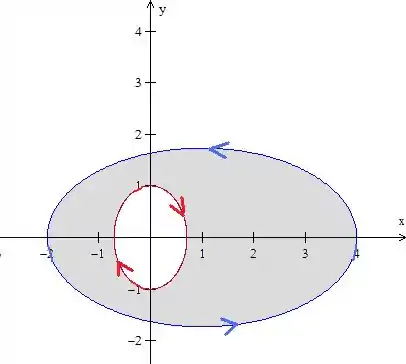
A elipse azul é e a vermelha é a curva auxiliar que criamos, podemos chamar de . Como as curvas estão com orientação positiva, sendo a região em cinza, podemos escrever:
Beleza?
Passo 3
Agora precisamos calcular a integral de linha na elipse menor (por isso escolhemos uma curva que tivesse semelhança com o campo, sacou?).
Vamos parametrizar a elipse usando coordenadas elípticas:
Esse coeficiente está aí para cancelar o na equação da elipse quando fazemos a mudança de variáveis, transformando a elipse em .
Como temos uma volta completa na elipse no sentido horário, vai de a .
Passo 4
Agora vamos derivar essa parametrização:
Passo 5
Escrevendo o campo
Nas variáveis da parametrização, temos:
Podemos, então, substituir os valores que encontramos na fórmula abaixo:
Passo 6
Agora vamos resolver isso aí:
Como
Nós temos