28) Seja de classe em , tal que , sejam , e . Calcule
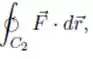
Sabendo que
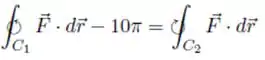
e
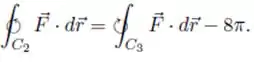
Passo 1
Eiiita! Que confusão de informações Rsrs! Para começarmos a destrinchar tuuuudo isso, comecemos pelo desenho dessas curvas (que são circunferências):
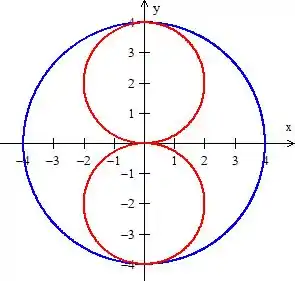
Bem! Repare que o que queremos é a integral de linha em girando no sentido anti-horário, pois
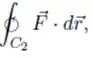
Note também que necessitamos de alguma coisa que une as informações das três integrais de linha, e essa “coisa” só pode ser o Teorema de Green:
Passo 2
Como podemos ver, a integral de linha que entra na igualdade de Green, é uma integral calculada na borda da região fechada :
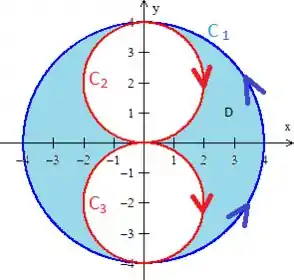
Como no nosso caso a borda são as curvas: ...
Olha que relação mara !
Agora tome cuidado, pois para essa igualdade estar verdadeira, a curva de fora tem que estar girando no sentido anti-horário e as demais, no sentido oposto:
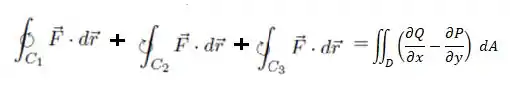
Passo 3
Como temos essa igualdade
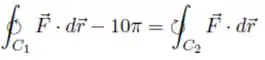
Se passarmos essa integral de linha em pro lado de cá, ela inverte o sentido de giro:
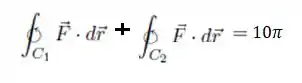
Passo 4
Com a segunda igualdade que obtivemos diretamente do enunciado:
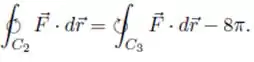
Jogando novamente a integral de linha de pra lá...
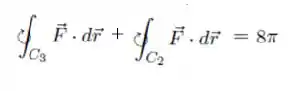
Passo 5
Com esses dois resultados...
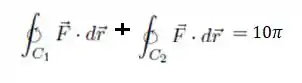
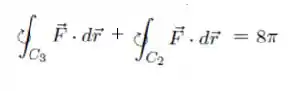
Podemos somar ambas as equações...
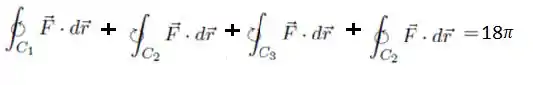
Ou seja, passando uma daquelas integrais em pra direita e invertendo o sinal...
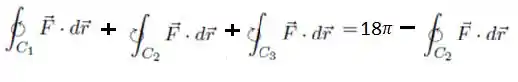
Substituindo esse resultado no teorema de Green...
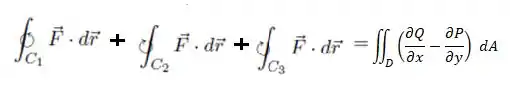
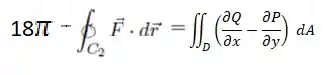
Se buscamos então a solução dessa integral de linha, calculemos o resultado da integral dupla e está tudo certo !
Passo 6
Como
Substituindo na integral dupla...
A integral de é a área da região :
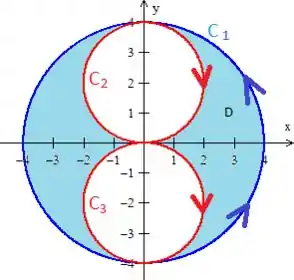
Que nada mais é do que a subtração da área da maior por vezes a área da menor (já que elas tem o mesmo raio)...
Quanto a integral em ... Vem comigo ;)
Passo 7
Cara, não sai calculando essa integral aí doidamente não. Essa é um daqueles momentos que se você parar para pensar um pouco durante minuto, pode te poupar hora:
Repare que a região tem uma simetria em relação ao eixo :
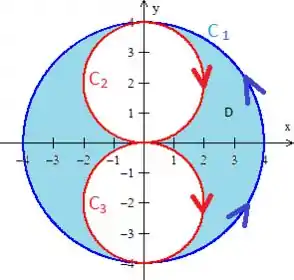
Essa simetria pode ser comprovada para o seu professor, fazendo a seguinte análise:
Os pontos com simetria no eixo são:
Se substituirmos ambos pontos nas equações das curvas que delimita a região (as três equações de circunferências), veremos que ambos dão a mesma equação:
O mesmo pode ser feito com as demais circunferências. Como a equação de fato continuou a mesma, essa simetria existe, sacou?
Outra coisa legal é que a função que estamos integrando: , é uma função ímpar, pois:
E cara, a integral de uma função ímpar dentro de uma região simétrica é :
Passo 8
Então... Como é vimos...
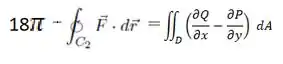
Isolando a integral de linha... E substituindo os valores: