Seja um campo vetorial tal que , contínuo em , onde é uma constante positiva. Suponha que
Onde é dada por , orientada no sentido anti-horário. Calcule a integral de linha vetorial
Onde é dada por, orientada no sentido anti-horário.
Passo 1
Vamos começar a resolver o nosso problema entendendo melhor quem são essas curvas dadas na questão.
Começando por ela, a curva , já sabemos que ela nos representa uma circunferência de raio e centrada na origem, dessa forma aqui
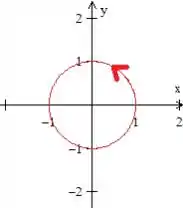
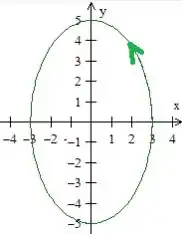
Já sabemos também que a nossa segunda curva, a , nos representa uma elipse. Mas como é mesmo a cara dessa elipse?
Se a gente colocar aqueles termos por baixo de e ao quadrado,
Observamos que essa elipse é uma elipse centrada na origem e com o eixo maior em cima de , dessa forma
Passo 2
Como buscamos a integral de linha sobre essa elipse e o cara não nos deu o campo, ele mesmo está nos sugerindo que façamos o problema pelo teorema de Green.
Mas a grande pergunta é, a gente está nas condições de aplicar o nosso amigo Green???
E a resposta é não ainda! Mas a gente vai chegar lá analisando suas condições e nos adaptando a ela, bora lá? :)
- A primeira condição nos fala que a gente tem que ter uma superfície fechada que esteja dentro das nossas curvas.
- A segunda, que a superfície deve estar orientada positivamente.
- A terceira, que a gente não pode ter singularidades, e a gente de fato não tem nenhuma dentro da nossa superfície entre a curva vermelha e a verde :)
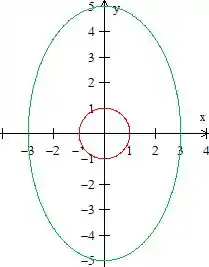
Como que a gente pode fazer isso? Sim! Colocando as duas curvas acima de um único gráfico e pegando a região entre elas! Assim:
Bem... se a gente estiver andando em cima dela, a gente tem que a ver toda do lado esquerdo, logo a curva verde tem que estar girando no sentido anti-horário e a vermelha no oposto:
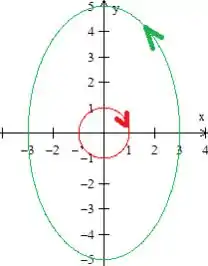
Passo 3
Estamos na condição de Green, bora aplicar o seu teorema!
Repare que no primeiro membro estamos calculando a integral de linha sobre a união das superfícies e que está negativa, pois estamos pegando a sua orientação inversa
Pela propriedade da soma
Temos o valor de
Logo, a solução do nosso problema é
Passo 4
Vamos agora encontrar a solução dessa última integral dupla
Colocando esse resultado na integral, teremos
Como é um número qualquer maior que , podemos tira-lo da integral
Lembre-se que nos representa a área da região que no nosso caso é a área da elipse menos a área da circunferência .
A área da circunferência a gente tem já que o conhecemos o raio
Um bizu para a gente encontrar a área da elipse sem ter que calcular uma integral é pegar os seus dois eixos e multiplicar por , dessa forma aqui
Logo teremos
Passo 5
Juntando todos esses ingredientes e retornando para o nosso problema inicial teremos