Calcule
Sendo o arco da curva que liga a
Passo 1
Vamos lá, essa questão parece que vai dar trabalho, vamos fazer com bastante calma pra não errar nenhum detalhe!
Geralmente, esses campos vetoriais que tem o mesmo denominador pra e possuem um rotacional simples. A conta não vai ser fácil, mas no final geralmente dá um número! Vamos calcular ele então e, em seguida, verificar que mudanças precisaremos fazer para aplicar o Teorema de Green!
Além disso, nosso campo vetorial possui uma singularidade no ponto , pois seu denominador fica igual a zero, se nosso domínio possuir esse ponto vamos ter que tirar essa singularidade de alguma forma, fica atento!
Passo 2
Calculando o rotacional do campo vetorial:
Para derivar isso em relação a vamos ter que fazer a regra do quociente, fica assim passo a passo:
Agora calculando a derivada de em relação a :
Portanto, podemos ver que nossas derivadas são iguais! Aplicando isso na fórmula do rotacional ficamos com:
Passo 3
Vamos analisar agora a nossa curva , ela é dada por , que tem seu gráfico, no intervalo de a , da seguinte forma:
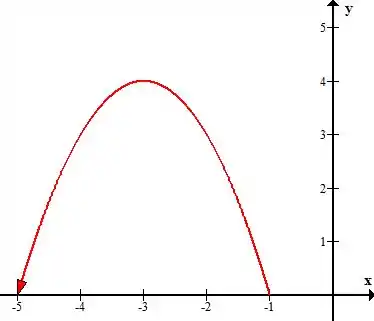
Ou seja, é uma curva aberta que podemos fechar facilmente com a reta no eixo de a . O problema de fazermos isso é que nosso campo vetorial possui uma singularidade no ponto , lembra? Vamos precisar criar uma circunferência ali pra tirar esse ponto, no final, vamos incluir duas novas curvas, vai ficar assim:
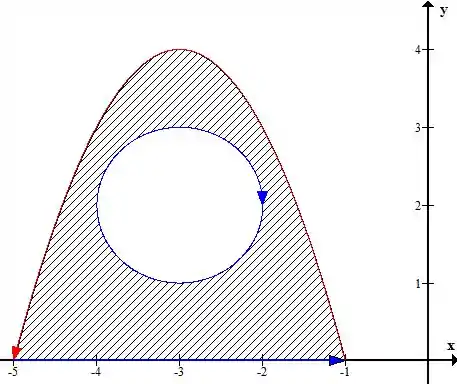
Onde as funções azuis foram as que tivemos que incluir para poder tirar a singularidade e fechar a curva . No Teorema de Green fica assim:
Como nosso rotacional é igual a zero, ficamos com:
Passo 4
Vamos agora encontrar as parametrizações das duas curvas que criamos.
A primeira é uma circunferência centralizada em , portanto sua parametrização é dada por:
Sua rotação está invertida de forma que a região sombreada fica à esquerda da função, lembra disso? Para o Teorema de Green ser válido, ao “caminhar” pela função, sua região deve estar a sua esquerda.
A segunda é uma reta onde e varia de a , portanto:
Passo 5
Vamos então calcular a integral de linha da nossa primeira curva.
Perceba que o denominador some porque fazemos:
Então nossa integral fica:
Passo 6
Vamos para a nossa segunda integral.
Nosso denominador vai ficar assim:
Voltando para a integral, sabendo que e
Para resolver essa integral vamos realizar uma substituição:
Para resolver isso vamos ter que usar um algebrismo que vai remeter a integral de um , se você não lembra, é assim:
Logo, se tivermos algo na forma na integral podemos resolvê-la. Para isso, vamos dividir nosso denominador por , assim:
Agora podemos integrar e dizer que:
“Arco cuja tangente é 1” é o ângulo e “Arco cuja tangente é ” é o ângulo de
Passo 7
Finalizando a questão, vamos voltar para o nosso Teorema de Green!