Considere o campo:
Determine onde é a fronteira do quadrado de vértices , , e orientada no sentido horário.
Passo 1
Bom, já deu para ver que calcular essa integral aí pela definição deve dar muito trabalho, né? Vamos tentar aplicar Green então. Temos:
Passo 2
Pelo Teorema de Green, considerando uma curva fechada orientada no sentido anti-horário e a região limitada por ela, temos:
Repare agora que o campo tem uma indeterminação: no ponto , por causa do denominador , que não pode se anular. Bem, na verdade, temos DUAS indeterminações, nos pontos e . Percebeu?
Então, para aplicarmos Green, nenhum desses pontos pode estar na nossa região! Mas como vamos fazer isso?
Olha de novo para o campo
Se você reparar, o denominador se parece muito com uma elipse, enquanto o denominador se parece muito com uma circuferência deslocada.
Ou seja, usando uma elipse para isolar os pontos que dão problema, um denominador vai ficar bonitinho, enquanto o outro vai ficar péssimo. O mesmo acontece se a gente usar uma circunferência deslocada.
Qual a solução? Separar esse campo em dois e usar, para cada um, uma curva!
Onde
Logo
Vamos então calcular a integral de cada parte do campo separadamente e depois somar as respostas!
Passo 3
Aplicando Green para a primeira integral:
Como é o campo que tem o denominador que parece uma elipse, vamos usar a elipse para isolar o ponto . Então, nossa região é essa aqui:
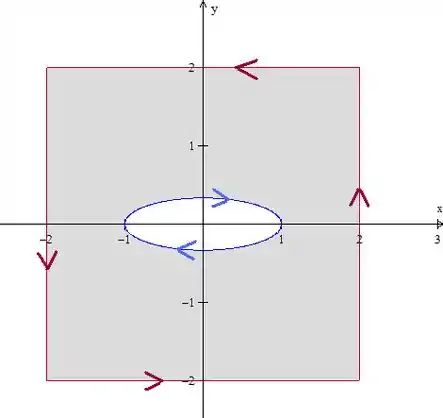
Cuidado com a orientação da fronteira, que deve ser positiva!
Portanto, a curva é a união do quadrado (no sentido contrário ao do problema) com a elipse e é a região em cinza.
Isolando o que queremos:
Mas queremos a integral em , não :
Como
Temos
Então, para encontrar a integral que queremos, basta calcular a integral na elipse .
Beleza, parametrizando em coordenadas elípticas, temos:
Como a elipse gira no sentido horário, vai de a .
Agora vamos derivar isso aí
Escrevendo o campo nas variáveis da parametrização:
Viu que o denominador virou ? A gente fez isso de propósito!
Podemos, então, substituir os valores que encontramos na fórmula abaixo:
Acabou? Calma que tem mais : (
Passo 4
Aplicando Green para a segunda integral:
Como é o campo que tem o denominador que parece uma circunferência deslocada, vamos usar a elipse para isolar o ponto .
Pera, porque usamos o raio e não ?! Porque, vendo na figura, uma circunferência de raio centrada em ia tangenciar a curva de fora! E isso não pode acontecer. Então, escolhemos um raio menor.
Então, nossa região é essa aqui:
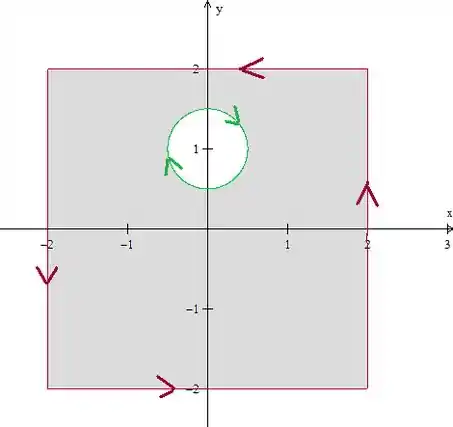
A curva é, portanto, a união de com a circunferência :
Isolando o que queremos:
Mas queremos a integral em , não :
Como
Isso nos dá
Então, precisamos calcular a integral na circunferência . Vamos parametrizá-la com coordenadas polares com raio e deslocadas para :
Como ela gira no sentido horário, vai de a . Derivando isso aqui:
Escrevendo o campo nas variáveis da parametrização:
Viu que o denominador simplificou de novo?
Podemos, então, substituir os valores que encontramos na fórmula abaixo:
Passo 5
Agora vamos juntar os resultados que encontramos: