Seja o campo e seja a curva que é fronteira da região limitada pelos gráficos das funções e percorrida no sentido horário. Calcule .
Passo 1
Vamos fazer um esboço dessa curva . Temos duas funções:
São duas parábolas com eixo de simetria paralelo ao . A segunda, na verdade, tem eixo de simetria no próprio eixo e tem concavidade para cima (por causa do sinal positivo no ). Já a primeira tem concavidade para baixo e é deslocada em relação ao eixo :
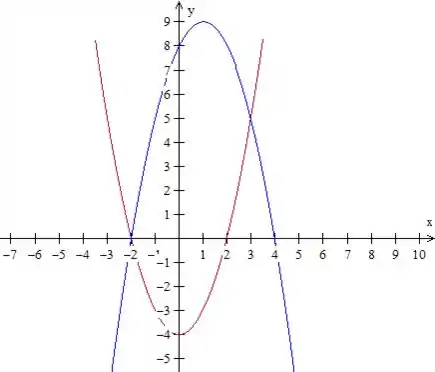
A curva é então isso aqui:
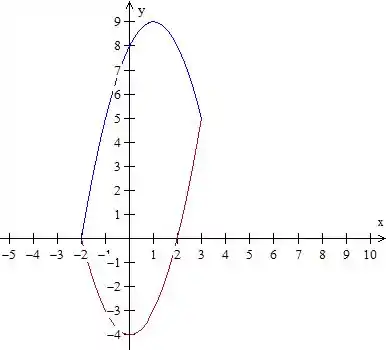
Como o enunciado fala, ela é percorrida no sentido horário.
Onde
Beleza? Então, podemos escrever:
Bom, já que temos uma curva fechada e um campo com expressão bizarra, vamos usar Green, né? Vamos fazer isso para cada parte do campo, separadamente.
Passo 2
Para o campo
Aqui nós temos um problema, se você reparar, o campo não está definido em , que pertence ao interior da nossa curva .
Vamos, então, fazer uma outra curva que envolva esse ponto (orientada no sentido horário) e considerar nossa região como o anel formado pelas duas curvas.
Beleza, conseguimos tirar o ponto da jogada tornando nossa região um anel, agora podemos aplicar Green.
Onde é o anel que está entre as duas curvas. Repare que, como é orientada no sentido horário (negativamente), tivemos que usar para aplicar o teorema. Já , é orientada positivamente (sentido horário). Isso é o mesmo que:
Temos então:
Ótimo, o campo é conservativo. Isso nos dá que:
Ok, agora vamos ver quem é .
Agora repara o seguinte, temo no denominador do campo... Parece uma elipse (deslocada), não é? Não seria muito bom se a nossa curva fosse uma elipse desse tipo? Olha só, vamos definir a elipse :
Repara que ela isola o ponto da nossa região, pois esse é o seu centro. Percebeu?
Sua parametrização, em coordenadas elípticas é:
Quando a gente aplicar isso aí na função do campo, as coisas vão ficar muito mais simples, porque o termo vai virar 1. Olha que lindo né.
Para nossa curva estar orientada positivamente, já vimos que a elipse deve ser percorrida no sentido horário, ou seja, vai desde até .
Vamos calcular agora a derivada dessa parametrização:
Então, usando a definição de integral de linha, podemos escrever o seguinte:
O campo
Escrito em termos da parametrização, fica
Substituindo o campo, a derivada da parametrização e os seus intervalos na integral, temos:
Calma que não acabou, ainda falta o campo !
Passo 3
Para o campo
Vamos lá, gente, força, quase acabando. O outro campo é o seguinte:
E nós queremos
Bom, como esse campo não tem nenhum problema com singularidade, podemos usar só a curva do enunciado para limitar nossa região, né? Vamos aplicar Green nesse aqui:
Temos então
Temos, de novo, a mesma questão da orientação aqui!
Onde é a região dentro de . Agora é só resolver essa integral dupla aí.
Vamos escrever a região como tipo I, está entre as equações das parábolas e entre e , como podemos ver na figura do passo 1. Para achar esses valores de , nós igualamos as equações das parábolas e descobrimos onde elas se encontram:
Levando para a integral, temos:
Passo 4
Como nós dissemos lá no início, a integral que queremos é dada por:
Substituindo os valores que encontramos