Calcule
Onde é a curva , , orientada de à
Passo 1
Vamos fazer um esboço da curva:
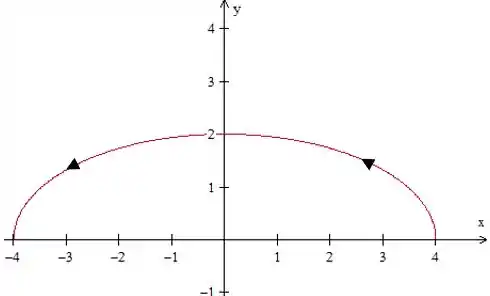
Essa integral de linha parece um pouco complicada de se calcular diretamente pela definição. Vamos, então, usar o Teorema de Green.
Repara que a curva não é fechada, para aplicarmos o teorema de Green devemos fechar essa curva.
Mas aqui temos um problema: o campo não está definido em toda a região dentro da elipse, pois temos uma descontinuidade na origem, se substituirmos na função teremos zero no denominador. O que faremos então? É simples, basta tirarmos a origem da jogada. Como temos que completar essa curva vamos pegar essa curva completando sem a origem.
Vamos fazer onde é uma circunferência de raio e centro na origem. A equação de vai ser
Pegamos uma circunferência de raio porque o gráfico vai ficar assim
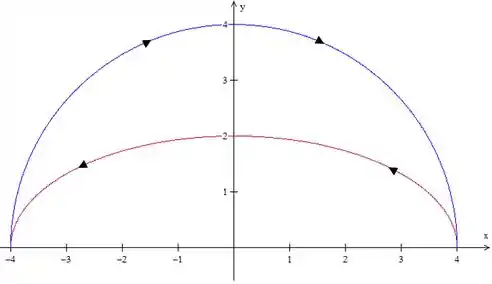
Veja que não é positivamente orientada, pois deixa a região a direita. Devemos usar então:
Passo 2
Vamos agora calcular :
Passo 3
Logo, temos que resolver o seguinte:
Temos que fazer a integral de linha e a integral dupla, vamos começar pela integral de linha.
Passo 4
Parametrizando a semicircunferência, temos:
Com variando de a
Substituindo esses valores na fórmula que vimos capítulo passado:
Temos:
Vamos separar essa integral em duas
Passo 5
Começando com
Lembrando que
Vamos ter,
Passo 6
Vamos para a outra integral agora
Vamos fazer a integral indetermina, ignorando por enquanto os limites e o
Vamos fazer
Então
E a integral vai ficar
Resolvendo a integral vamos ter
Voltando para
Vamos voltar para a integral com os limites e o
Passo 7
Então, nossa integral de linha resulta em:
Passo 8
Vamos agora para a integral dupla,
Onde é a parte de dentro da circunferência e de fora da elipse
Antes de tudo vemos que essa integral vai ser
Passo 9
Vamos voltar para o gráfico que vimos antes.
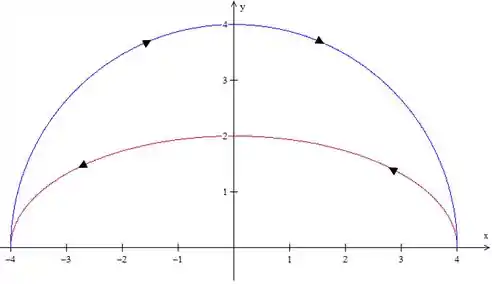
A área de vai ser a área da semicircunferência menos a da semielipse, ou seja
Passo 10
Vamos agora para a integral com
Como temos várias coisas circulares é jogo usarmos coordenadas polares né? Então
A equação da elipse é:
Então, nossos limites são:
E como estamos no primeiro e segundo quadrantes:
Substituindo na integral:
Integrando em :
Separando em duas integrais:
Os novos limites de integração são:
Opa, já deu pra ver o que vai rolar né? Uma integral indo de até vale !! Então:
Passo 11
E ficamos com:
Passo 12
Agora pra finalizar (FINALMENTE!!!!):