Calcule a seguinte integral de linha de campo vetorial:
Ao longo da curva , união das curvas definidas por:
- , a curva percorrida no sentido horário,
- , a curva percorrida no sentido anti-horário.
Passo 1
Antes de tudo, vamos fazer um esboço dessas curvas para entender melhor o problema:
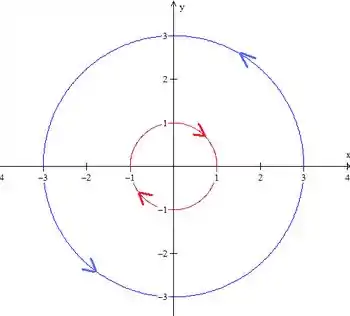
Como temos duas curvas com expressões diferentes, vamos separar a integral:
Não podemos aplicar Green direto nessa região porque, se você reparar, temos duas singularidades no campo que estão na região entre e .
Passo 2
Agora vamos dar uma olhada no campo:
Percebeu que o primeiro termo da componente é bem parecido com o primeiro da componente ? Assim como o segundo da com o segundo da .
Isso nos leva a pensar que, dividindo esse campo em duas partes, podemos facilitar nossas contas (isso vai nos ajudar mais à frente, prometo!). Temos então:
(Vemos que o campo não está definido em e que não está definido em .
Isso nos dá:
Beleza?
Passo 3
Agora, temos o seguinte:
Ótimo, isso simplifica muito as coisas!
Passo 4
Agora vamos com calma, vamos analisar as integrais uma a uma.
Onde , como sabemos, é a circunferência de raio centrada na origem. Como está definido dentro de , podemos aplicar Green:
Onde é a região limitada por .
Passo 5
Agora vamos para a segunda integral
Aqui nos temos o mesmo que no passo anterior, como está definido dentro de , aplicamos Green:
Passo 6
Agora vamos para a terceira integral
Para essa integral a história já é diferente, porque o ponto em que o campo não está definido , está dentro de (dá uma olhadinha na figura no passo 1).
Então, nós vamos envolver esse ponto com uma terceira circunferência centrada nele:
Então, sendo a região entre as circunferências e , podemos aplicar Green:
Como gira no sentido anti-horário, para termos orientação positiva, gira no sentido horário. Isso nos dá:
Agora, para calcular essa integral de linha em , vamos começar parametrizando essa curva em coordenadas polares deslocadas com :
Como o sentido é horário, vai de a .
Derivando isso aí
Agora, vamos levar isso para a fórmula:
Logo
Passo 7
Agora, temos a quarta integral:
Como não está definido em , precisamos fazer o mesmo que no passo anterior para aplicar Green. Vamos envolver esse ponto com a curva :
Então, sendo a região entre as circunferências e , podemos aplicar Green:
Como gira no sentido anti-horário, para termos orientação positiva, gira no sentido horário. Isso nos dá:
Agora, para calcular essa integral de linha em , vamos começar parametrizando essa curva em coordenadas polares deslocadas com :
Como o sentido é horário, vai de a .
Derivando isso aí
Agora, vamos levar isso para a fórmula:
Logo
Passo 8
Agora juntamos tudo o que temos