Exercícios Resolvidos de Coeficientes Constantes Não Homogênea-Coeficientes Indeterminados
Ver TeoriaEnunciado
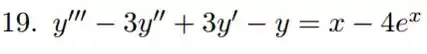
Passo 1
Essa é uma EDO não-homogênea. Mas vamos primeiro ignorar aquela função enjoada ali do lado direito da equação e vamos resolver como se fosse homogênea.
Determinando a equação característica
De cara vemos que uma das soluções é
Passo 2
Sabendo uma das raízes, podemos usar o método de Briot-Ruffini para diminuir o grau dessa equação. Fica algo assim:
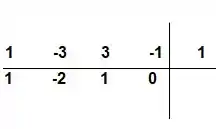
Então a equação reduzida será
Que se determinarmos as raízes encontramos
Então esta é uma raízes tripla e a solução homogênea é:
Passo 3
Agora chega de ignorar as funções do lado direito.
Perceba que aí temos uma soma de duas funções então temos que pensar em dois chutes para a solução particular
Mas olha que uma solução já aparece na solução homogênea então temos que multiplicar por para que a solução não apareça novamente. Então:
E
Passo 4
O próximo passo é derivar nosso chute para a solução particular e aplicar na EDO.
Aplicando na EDO temos
Simplificando podemos chegar em que
Enfim, chegamos na solução particular que é
Passo 5
Sabemos que
Então