Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Coeficientes Constantes Não Homogênea-Coeficientes Indeterminados

Ver Teoria
Exercício 1412345678910111213151617181920212223242526272829

Enunciado

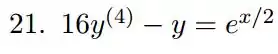
Passo 1

Lá vamos nós resolver mais uma EDO não homogênea. Primeiro, vamos resolver ignorando a parte não homogênea.

16 y i v - y = 0

A equação característica será

16 r 4 - 1 = 0

Que é uma equação biquadrada, que pode ser resolvida substituindo x = r 2

16 x 2 - 1 = 0

x = ± 1 4

Então

r = ± 1 2   e   r = ± 1 2 i

Então nossa solução homogênea será

y h x = C 1 e x 2 + C 2 e - x 2 + C 3 cos ⁡ x 2 + C 4 sen ⁡ x 2

Passo 2

Agora precisamos encontrar a solução particular, neste caso e x 2 já aparece na solução homogênea, então vamos chutar

y p = a x e x 2

E derivar nosso “chute” para aplicar na EDO

y p ' = a e x 2 + a x 2 e x 2

y p ' ' = a 2 e x 2 + e x 2 2 + a x 4 e x 2 = a e x 2 + a x 4 e x 2

y p ' ' ' = a 2 e x 2 + a e x 2 4 + a x 8 e x 2 = 3 a 4 e x 2 + a x 8 e x 2

y p i v = 3 a 8 e x 2 + a e x 2 8 + a x 16 e x 2 = a 2 e x 2 + a x 16 e x 2

Aplicando na equação

8 a e x 2 + a x e x 2 - a x e x 2 = e x 2

8 a = 1

a = 1 8

Logo, a solução particular é

y p x = 1 8 x e x 2

Passo 3

Sabemos que

y x = y h x + y p x

Logo,

y x = C 1 e x 2 + C 2 e - x 2 + C 3 cos ⁡ x 2 + C 4 sen ⁡ x 2 + 1 8 x e x 2

Resposta

y x = C 1 e x 2 + C 2 e - x 2 + C 3 cos ⁡ x 2 + C 4 sen ⁡ x 2 + 1 8 x e x 2

Exercícios de Livros Relacionados

Use o método dos aniquiladores para encontras a forma de uma solução particular Y t para cada uma das equações nos problemas de 13 a 18. Não calcule os coeficientes.
O Método dos Aniquiladores. Nos problemas de 20 a 22, consideramos outra maneira de chegar a uma forma adequada para Y ( t ) para usar no método dos coeficientes indeterminados. O procedimento baseia-
19. Considere a equação diferencial linear não homogênea de ordem n a 0 y n + a 1 y n - 1 + … + a n y = g t ( i ) em que a 0 ,...,a n são constantes. Verifique que, se g ( t ) tiver a forma e α t b 0
Em cada um dos problemas de 13 a 18, determine uma forma adequada para Y ( t ) se for utilizado o método dos coeficientes indeterminados. Não calcule as constantes.17. y ( 4 ) -y ' ' ' - y ' ' + y ' =
Em cada um dos problemas de 13 a 18, determine uma forma adequada para Y ( t ) se for utilizado o método dos coeficientes indeterminados. Não calcule as constantes.18. y ( 4 ) + 2 y ' ' ' + 2 y ' ' =