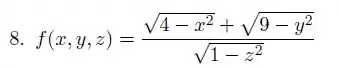
Passo 1
Vishh Maria, quanta restrição! É raíz, é denominador, é raíz NO denominador...
Ainda bem que a gente sabe bem resolver isso, uhul
Sabemos que o que está dentro da raíz tem que ser maior ou igual a zero e o que está no denominador tem que ser diferente de zero. Assim, quando temos raíz no denominador, o que tá dentro só vai poder ser maior do que zero, por causa daquele mandamento divino de “Jamais dividirás por zero”. Beleza?!
Vamos começar então pelas raízes do numerador: o que tá dentro delas tem que ser maior ou igual a zero, assim
E
Se fossem igualdades, passando constante pra um lado e variável pra outro e tirando a raíz, ficaríamos com
Mas, como temos uma desigualdade, isso signifca que
Que é a mesma coisa que usar módulo e dizer:
Fazendo exatamente as mesmas coisas pra raíz do denominador, mas agora considerando que o que está dentro dela tem que ser só maior do que zero (e não maior ou igual), temos
Assim, o domínio da nossa função é a interseção dessas três coisas:
Passo 2
Beleza, agora temos que desenhar isso.
Vamos pensar. Se fossem igualdades, a gente teria 6 retas:
Como estamos no , essas retas estão no espaço. Mas, além disso, como temos desigualdades, o que temos na verdade é o espaço definido entre essas retas, ou seja, planos.
Assim
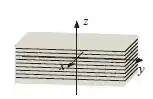
Resposta
![]()