Determine e faça o esboço do domínio da função:
Passo 1
Beleza, vamos encontrar o domínio dessa! Lembre, comece sempre procurando quais são as restrições da função. Nesse caso, temos que o denominador da função não pode valer . Assim, tendo a função
Passo 2
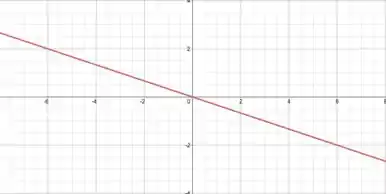
Pronto! Agora é só passar o pro outro lado e...
Interpretemos isso. Se fosse um sinal de igual, teríamos uma reta, certo? Como é um sinal de diferente, temos tudo menos essa mesma reta! Ou seja, nosso domínio é todo o plano, menos a reta :
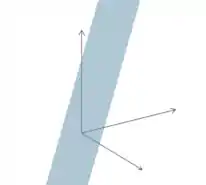
Passo 3
Po, mas você me disse na teoria que o domínio estaria no espaço e não no plano! Calma jovem gafanhoto!
Agora vem o “detalhe” percebeu que o não aparece na nossa função? Isso significa que para qualquer valor de e , teremos todos os valores possíveis para ! Como encontramos uma reta no passo anterior como sendo a restrição da nossa função, então essa restrição se expande para um plano! Veja, no gráfico da nossa função, que o domínio é todo o menos o plano
Resposta
O domínio é todo o , excluindo o plano , mostrado na figura abaixo