Uma partícula de massa desloca-se sobre uma mesa horizontal, sem atrito, com velocidade . Num certo instante ela se desintegra espontaneamente em três fragmentos de massas , e com velocidades , e , com na mesma direção e sentido oposto a e perpendicular a e como mostrado na figura abaixo. O módulo da velocidade do fragmento de massa é . Em termos dos dados do problema, e , e utilizando o sistema de eixos da figura determine:
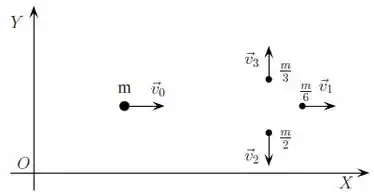
a) Os vetores velocidade e .
b) Os vetores velocidade dos fragmentos em relação ao referencial do centro de massa do sistema.
Passo 1
Quando essa partícula se desintegra em fragmentos, podemos tratar como se fosse uma colisão e dizer que seu momento linear se conserva:
Mas por que se conserva?
Como a mesa está na horizontal, as únicas forças externas atuando sobre a partícula/fragmentos (peso e normal) se cancelam, não tendo uma força resultante externa atuando.
Na letra (a), queremos achar e , então vamos aplicar na conservação do momento linear.
Passo 2
Podemos trabalhar separadamente com o momento linear na direção do eixo e o momento na direção do eixo .
Vamos começar com o eixo :
Inicialmente, temos apenas o momento linear da partícula, com velocidade na horizontal:
Enquanto no final, o único fragmento com velocidade na horizontal é o com velocidade :
Então, ficamos com:
Achamos o módulo da velocidade . Escrevendo vetorialmente, essa velocidade ganhará o vetor unitário , pois está na horizontal.
Passo 3
Vamos partir para o eixo , agora:
Inicialmente não há nenhuma componente de velocidade na vertical, então:
Já no final, temos tanto o fragmento com quanto o fragmento com :
Igualando os momentos lineares inicial e final:
O enunciado nos deu que :
Escrevendo os dois vetorialmente, vamos acrescentar o vetor unitário , pois as velocidades estão na vertical. Lembrando que está para baixo, então ela é negativa:
Passo 4
Já na letra (b), queremos a velocidade de cada fragmento com relação ao centro de massa do sistema.
Para isso, precisamos calcular a para esse sistema.
Poderíamos fazer isso a partir da fórmula de velocidade do centro de massa, que é nada menos do que uma média entre as velocidades de cada fragmento:
Porém, tem um jeito bem mais simples de descobrir essa velocidade do centro de massa...
Lembra que o momento linear do sistema se conserva antes e depois da fragmentação?
Sim, né.
Então, como o momento linear do sistema se conserva, isso significa que a velocidade do centro de massa também se conserva.
Ou seja, podemos em vez de olhar para a situação depois da fragmentação, podemos olhar para um instante anterior a isso.
Inicialmente o sistema é apenas a partícula andando com velocidade , logo a velocidade do centro de massa será a própria velocidade da partícula:
Passo 5
Agora que já sabemos a velocidade do centro de massa, podemos encontrar a velocidade relativa de cada um dos fragmentos.
Basta pegar a velocidade de cada fragmento com relação a um observador externo e subtrair da velocidade do centro de massa com relação ao mesmo observador externo:
Então, para o primeiro fragmento:
Já o segundo fragmento:
E por últiimo, o terceiro fragmento:
Resposta
(a)
(b)