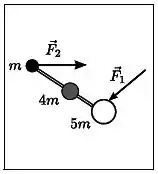
Três pequenos discos de massas , e estão ligados por barras ideais (rígidas) de massas desprezíveis. Este sistema está apoiado sobre uma mesa horizontal lisa. Em um dado instante aplicam-se duas forças, e , sobre os discos de massas e , respectivamente. As forças são paralelas ao plano da mesa como mostra a figura (mesa vista de cima). No instante considerado a aceleração do centro de massa do sistema constituído pelos discos e pelas barras é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h) O centro de massa permanece em repouso.
Passo 1
Essa questão pode tentar te confundir um pouco, mas ela é bem simples.
Se liga na segunda lei de Newton:
Essa lei diz que a força resultante sobre um corpo, ou seja, o somatório de forças sobre ele é igual à massa vezes a aceleração.
Repare que ela originalmente é escrita na forma vetorial, por isso temos a setinha na e na .
Outro detalhe importante é que somamos dois vetores com um sinal de independente de suas direções. A soma de um vetor com um vetor é:
Mas ué? E quando esses caras estão em sentidos opostos?
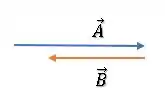
A gente não pegava o primeiro e subtraia do segundo?
Não vamos confundir as coisas. Quando queremos calcular o módulo do vetor resultante, ai consideramos as direções deles dentro dos sinais:
Entretanto, a soma deles em notação vetorial ainda será:
Passo 2
Beleza, vamos aplicar a segunda lei de Newton no nosso problema.
Quando temos um sistema de partículas, podemos considerar que toda a massa está em apenas um ponto (centro de massa) e aplicar a segunda lei para essa nova “partícula”.
Então, a força resultante no sistema será igual à soma de massas vezes a aceleração do centro de massa:
Então, temos que:
A força resultante no sistema será a soma vetorial de com :
Assim:
Agora basta somarmos a massa de todas as partículas:
Ficamos com a alternativa (a).
Resposta
Letra (a)