Um homem de massa está em pé sobre uma das extremidades de uma prancha que flutua num lago de águas calmas. A massa da prancha, que é distribuída de maneira uniforme em seu comprimento , é . O homem começa a andar em direção à outra extremidade da prancha. Desprezando o atrito entre água e a prancha, determine a distância que a prancha percorre durante o percurso do homem de uma extremidade à outra da prancha.
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Vamos começar com um desenho da situação. O homem se encontra parado na extremidade de uma prancha:
Como esse sistema está inicialment em equilíbrio, a força resultante externa é nula.
Mas e quando ele começar a se mover?
Quando o homem caminha sobre a tábua, ele exerce uma força na tábua para a esquerda, porém, a tábua exerce uma força de mesma intensidade no homem para a direita (ação e reação). Assim, essas forças se anulam (são forças internas) e o nosso sistema continua em equilíbrio.
Então, podemos considerar que o momento linear se conserva.
Mas pra que eu falei isso tudo?
Ah, é porque se o nosso sistema estava em repouso inicialmente, quando o homem caminha sobre a prancha, o nosso sistema continuará em repouso e, assim, a posição do centro de massa estará no mesmo lugar.
Podemos usar isso para achar uma relação entre o quanto cada um dos dois (homem e prancha) se deslocou.
Passo 2
Calculando a posição do centro de massa.
Vamos considerar a origem na posição em que a extremidade esquerda da prancha se encontra:
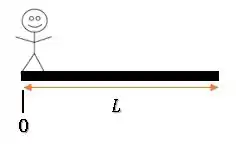
A posição do homem será:
Como a prancha tem sua massa distribuida uniformemente (homogênea), podemos concetrar sua massa no seu ponto médio, logo a posição do centro de massa da prancha é:
Com isso, podemos calcular a posição do centro de massa do conjunto:
Passo 3
Agora, vamos olhar para a situação após o homem se deslocar até a outra extremidade da prancha.
A prancha se deslocou para a esquerda da origem, então a posição de seu centro de massa será:
Agora dá uma olhada no homem:
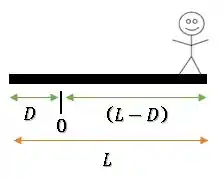
Se a prancha recuou uma distância , sua posição com relação à origem será:
Então, podemos dizer que a posição do centro de massa nesse sistema se encontra na mesma posição que já calculamos e assim conseguimos achar a distância .
Cortanto e multiplicando cruzado, temos:
Logo, a prancha se desloca uma distância igual a .
Resposta
Letra (a)