As quatro partículas, cujas velocidades são mostradas na figura, têm a mesma massa e movem-se com a mesma rapidez constante.
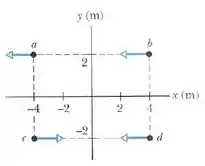
O seguinte par de partículas forma um sistema cujo centro de massa permanece em repouso na origem:
(A) a e b
(B) a e c
(C) b e c
(D) a e d
(E) b e d
Passo 1
Calculamos o centro de massa da seguinte forma:
Eixo x:
Eixo y:
Como as partículas possuem a mesma massa, para que sejam nulos as partículas precisam sempre possuírem coordenas x e y com mesmo valor e sinais opostos. Das partículas fornecidas, isto só é possível para as partículas b e c .