Duas pessoas, de mesma massa , estão de pé e presas às extremidades opostas de uma prancha, de comprimento e massa desprezível, que inicialmente se encontra em repouso sobre uma pista de gelo, como mostrado na figura. A pessoa da direita joga, com certa velocidade horizontal, uma bola de massa em direção à outra pessoa que consegue pegá-la. Despreze os efeitos da resistência do ar e do atrito entre a prancha e a pista de gelo. Para um observador parado na borda da pista:

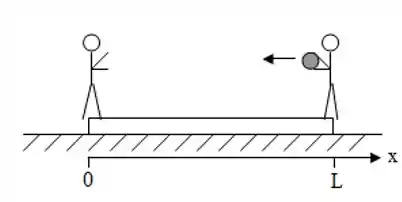
(a) Encontre a equação que descreve a posição do centro de massa () do conjunto prancha + pessoas + bola enquanto a bola vai da direita para a esquerda. Justifique sua resposta com argumentos físicos.

(b) Encontre as equações da velocidade e da posição do centro da prancha (que inicialmente vale ) enquanto a bola vai da direita para a esquerda, em função das massas e da velocidade da bola.

(c) Determine a posição da pessoa da direita, no momento em que a bola é agarrada pela pessoa da esquerda, usando o referencial da figura.

(d) O que acontece com o conjunto prancha + pessoas + bola após que a pessoa da esquerda agarrou a bola? Justifique sua resposta com argumentos físicos.

(b)

Como o não pode se deslocar, enquanto a bola se desloca da direita para a esquerda, a prancha deve se deslocar da esquerda para a direita. Durante o movimento da bola, teremos a velocidade da bola e a velocidade da prancha que por conta do contato, será também, a velocidade das pessoas.

Pronto, já temos a velocidade da prancha, como não possui forças externas atuando, essa velocidade é constante e deve obedecer a fórmula:

Substituindo os dados do problema:

(c)

No final do movimento, as duas pessoas se deslocaram para a direita de uma mesma distância em relação às suas posições iniciais.

E como a posição do centro de massa é fixa, podemos dizer que:

Logo, como a pessoa da direita estará na posição:

(d)

Como a posição do é constante, o conjunto prancha + pessoas + bola depois que a pessoa da esquerda agarrou a bola permanece em repouso.