Calculadoras científicas simples são autorizadas.
Eduardo e Mônica resolvem fazer um romântico passeio de canoa. Eduardo, com , senta-se em um extremo da canoa, enquanto Mônica, com , senta-se no outro extremo. A ponta em que está sentado Eduardo dista de da margem. O barco tem um comprimento total de e massa de . Quebrando o romantismo, Eduardo se dá conta de que esqueceu os remos na margem e tem a seguinte ideia: se eles trocam de lugar, o barco deverá se mover em direção à margem e com isto Mônica pode tentar alcançar os remos. Para não perderem o equilíbrio, primeiro caminhou Mônica, depois Eduardo.
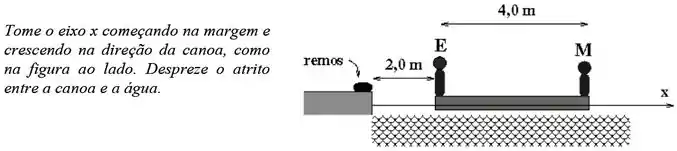
a) Durante o deslocamento de Mônica, a canoa tem uma velocidade escalar de em relação à água. Qual é a velocidade de Mônica, também em relação à água?
b) O braço de Mônica tem 60 cm. Ao final do deslocamento de ambos, ela consegue alcançar os remos? (despreze a variação do centro de massa de Mônica ao esticar um braço)
Justifique claramente o desenvolvimento em ambos itens!
Passo 1
a)
Temos um sistema de partículas composto pela canoa, por Eduardo e Mônica. Vou chamá-los de e , assim quando eu botar, por exemplo, , é a massa do Eduardo, beleza?
Repare que não há nenhuma força externa atuando (ele diz pra desprezar o atrito). Sabemos que nesse caso, a velocidade do centro de massa é constante!
E antes da Mônica começar a mexer, estão todos parados: .
Então durante o deslocamento da Mônica, também vamos ter:
E a fórmula geral da velocidade do centro de massa é dada por:
Então vamos aplicar isso!
Passo 2
Mas vamos primeiro dar uma olhada nos dados do enunciado:
E durante o deslocamento da Mônica, temos
O Eduardo está parado em relação à canoa, então
Passo 3
Show! Vamos às contas:
O eixo aponta pra direita e a Mônica está se movendo pra esquerda, então a velocidade dela tem que dar negativo mesmo!
Passo 4
b)
A velocidade do centro de massa é então a posição do CM não muda!
E a fórmula do é:
Passo 5
Vamos começar calculando a posição do CM antes de qualquer deslocamento, beleza?
O CM da canoa é no meio da canoa (assumimos que ela é homogênea), então .
Também temos e . Portanto,
Passo 6
Excelente! Agora vamos achar a posição do CM do sistema depois de Eduardo e Mônica terem terminado de trocar de lugar. Mas a gente não sabe a que distância da borda a canoa ficou.
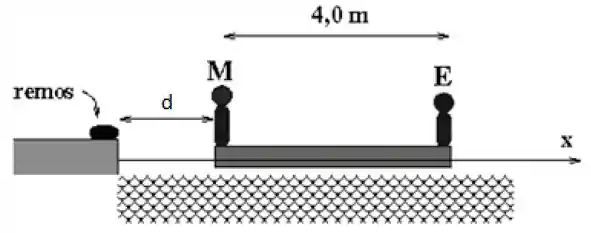
Então vamos expressar e em função desse .
- A canoa tem de comprimento, e o seu CM fica no meio dela, portanto a uma distância da borda.
- O Eduardo foi parar do outro lado da canoa, então .
- A Mônica está na ponta da canoa mais próxima da borda, logo .
Passo 7
Agora só resta calcular! Vamos ter
Passo 8
Show, estamos quase acabando! Vimos que . Logo,
E o braço da Mônica só tem então ela não vai conseguir alcançar os remos! Pois é Mônica, não adianta fazer medicina e falar alemão se o seu braço é curto! :)
Resposta
a)
b) Não.